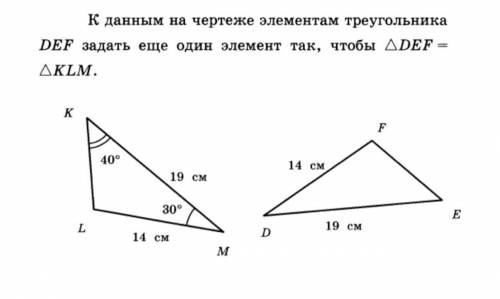
К данным на чертеже элементам треугольника DEF задать еще один элемент так, чтобы
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.Ұлы жібек жолы қай жерден басталды?2.Ұлы жібек жолы пайда болды;3.Ұлы...
2 - С чем связана смена времён года на Земле?Приведи 2 причины...
1 - Літературний герой з якими хотів товаришувати 15 речень...
1 - Почему в опыте отражённом на рисунке 243 мы использовали металлический...
1 - Постройте дерево, соответствующее арифметическому выражению (5*b+a)/(2*a+3*b+6)...
1 - Запиши в тетради признаки наступления весны у растений, которые...
1 - Найдите частную производную первого порядка z=x^3+5xy^2-5x-2y...
2 - 3. Длина прямоугольникав 3 раза больше егоширины. Ширина короче...
2 - Шеңбер бойында жататын А нүктесі арқылы AB диаметрі мен AC хордасыжүргізілген....
3 - Впишите в текст пропущенные слова. Вес тела следует отличать от...
2
Чтобы задать еще один элемент треугольника DEF, можно использовать различные величины: углы, высоты, биссектрисы, медианы и т.д.
В данном случае, учитывая известные стороны треугольника, можно использовать теорему косинусов для нахождения одного из углов.
Теорема косинусов гласит:
c^2 = a^2 + b^2 - 2ab*cos(C), где c - сторона противолежащая углу С, а и b - остальные стороны треугольника.
Для нашего треугольника имеем:
DE^2 = EF^2 + FD^2 - 2*EF*FD*cos(∠DEF) \[\circ\]
Подставляя известные значения:
4^2 = 3^2 + 5^2 - 2*3*5*cos(∠DEF) \[\circ\]
Решаем уравнение относительно cos(∠DEF):
16 = 9 + 25 - 30*cos(∠DEF)
30*cos(∠DEF) = 25 + 9 - 16
30*cos(∠DEF) = 18
cos(∠DEF) = 18/30
cos(∠DEF) = 0.6
Теперь, используя таблицу значений тригонометрических функций, можем найти угол ∠DEF, соответствующий данному значению косинуса. Получаем, что ∠DEF = 53.13° (округляя до второго знака после запятой).
Таким образом, еще одним элементом, который можно задать для треугольника DEF, является угол ∠DEF = 53.13°.