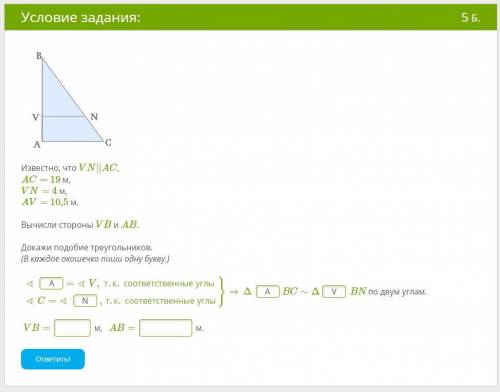
Известно, что VN||AC,
AC= 19 м,
VN= 4 м,
AV= 10,5 м.

Вычисли стороны VB и AB.

Добрый день! Рассмотрим данный геометрический вопрос поэтапно.

1. Для начала, посмотрим на изображение и обозначим все величины, которые даны в условии задачи. У нас имеются следующие значения:
- AC = 19 м
- VN = 4 м
- AV = 10,5 м

2. Дано, что VN параллельна AC. Из этой информации можно сделать вывод, что треугольник AVB и треугольник ACB подобны. Почему? Потому что если две прямые параллельны, то все прямые, проведенные через них, также будут параллельны.

3. Поэтому, пропорции сторон треугольников AVB и ACB равны:
AB/AC = VB/VN = AV/AB

4. Теперь, найдем значения VB и AB. Для этого используем первую пропорцию:
AB/AC = VB/VN

Подставляем известные значения:
AB/19 = VB/4

5. Теперь, чтобы найти значения AB и VB, мы должны избавиться от дробей в равенстве. Для этого умножим значения слева и справа на 4 и 19 соответственно:
AB * 4 = 19 * VB

6. Получаем уравнение:
4AB = 19VB

7. Из условия задачи также известно, что AV = 10,5 м. Мы можем использовать это значение, чтобы выразить AB в терминах VB:
AB = AV - VB

8. Подставляем значение AB в предыдущее уравнение:
4 (AV - VB) = 19VB

9. Раскрываем скобки и получаем:
4AV - 4VB = 19VB

10. Переносим все члены с VB на одну сторону уравнения:
4AV = 23VB

11. Теперь, чтобы найти значения AB и VB, мы делим оба члена на 4AV:
(4AV)/(4AV) = (23VB)/(4AV)

12. Получаем:
1 = (23VB)/(4AV)

13. Теперь, чтобы найти значение VB, делим оба члена на (23/4)AV:
VB = (4AV) / (23/4)

14. Упрощаем выражение:
VB = (4 * 10,5) / (23/4)

15. VB = 42 / (23/4)

16. Чтобы разделить число на дробь, надо умножить его на обратную дробь:
VB = 42 * (4/23)

17. Упрощаем выражение:
VB = 168/23

18. VB ≈ 7,3 м

19. Теперь, чтобы найти значение AB, подставим найденное значение VB в любую из пропорций:
AB/19 = VB/4

20. Подставляем известные значения:
AB/19 = 7,3/4

21. Чтобы найти AB, умножим оба члена на 19:
AB = (7,3/4) * 19

22. AB ≈ 13,4 м

Таким образом, сторона VB равна примерно 7,3 м, а сторона AB равна примерно 13,4 м.