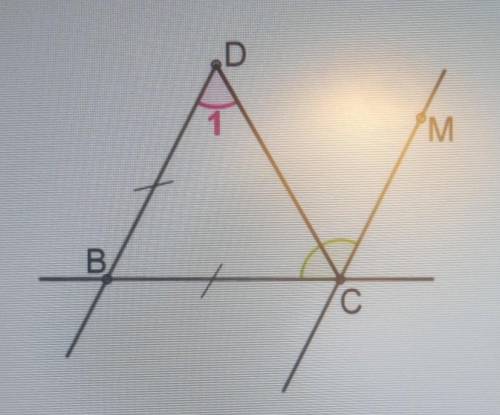
Известно, что в данной ситуации: DB=BC
DB∥MC
∡BCM=160°

Определи величину∡1.

∡1=__°

Для решения данной задачи, нам необходимо использовать знания о параллельных прямых и углах.

Из условия задачи можно заметить, что отрезок DB равен отрезку BC (DB=BC), что говорит нам о равенстве этих сторон треугольника BDC.

Также из условия мы знаем, что прямые DB и MC параллельны (DB∥MC).

Теперь обратимся к углу ∡BCM, который равен 160°. Мы можем заметить, что это внутренний угол треугольника BDC, образованный прямыми DB и BC.

Поскольку DB∥MC, то внутренний угол BDC также будет равен 160°, поскольку он соответственный угол по отношению к ∡BCM.

Теперь мы можем решить задачу, определив угол ∡1.

Первым шагом нам нужно найти внутренний угол треугольника BDC, который можно назвать ∡2. Мы можем сделать это, вычтя из 180° внутренний угол треугольника BDC (∡2), равный 160°:

∡2 = 180° - ∡BCM
∡2 = 180° - 160°
∡2 = 20°

Теперь мы можем определить угол ∡1, используя тот факт, что сумма углов треугольника равна 180°:

∡1 = 180° - ∡2
∡1 = 180° - 20°
∡1 = 160°

Таким образом, величина угла ∡1 равна 160°.