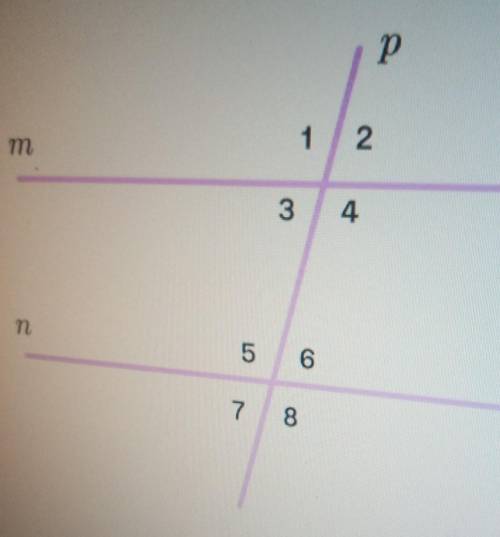
Известно что m||n, угол 1 = 142°. Найди все остальные углы Угол 1 и 2 смежные, значит угол 2 = °
Угол 1 и 3 односторонний, значит угол 3= °
Угол 2 и 4 односторонние, значит угол 4= °
Угол 5 и 4 накрест лежащие, значит угол 5 = °
Угол 6 и 4 односторонние, значит угол 6= °
Угол 6 и 7 вертикальные, значит угол 7= °
Угол 8 и 7 смежные, значит угол 8= °​

Значит его 2 равно 71

Для решения данной задачи, в которой имеются несколько параллельных и пересекающихся прямых, а также углы, необходимо воспользоваться знаниями о свойствах параллельных прямых и соответствующих углах.

Исходя из информации, что m || n и угол 1 = 142°, можно сделать следующие выводы:

1. Угол 1 и 2 смежные, следовательно, угол 2 = угол 1 = 142°.

2. Угол 1 и 3 являются односторонними углами - это означает, что они в сумме дают 180°. Таким образом, угол 3 = 180° - угол 1 = 180° - 142° = 38°.

3. Угол 2 и 4 также являются односторонними углами, значит, они также в сумме дают 180°. Следовательно, угол 4 = 180° - угол 2 = 180° - 142° = 38°.

4. Угол 5 и 4 являются накрест лежащими углами. По свойству параллельных прямых и накрест лежащих углов, они равны между собой. Поэтому угол 5 = угол 4 = 38°.

5. Угол 6 и 4 являются односторонними углами. Из свойства параллельных прямых и односторонних углов следует, что сумма этих углов равна 180°. Следовательно, угол 6 = 180° - угол 4 = 180° - 38° = 142°.

6. Угол 6 и 7 являются вертикальными углами - они равны между собой. Следовательно, угол 7 = угол 6 = 142°.

7. Угол 8 и 7 являются смежными углами - они лежат на смежных сторонах пересекающихся прямых и имеют общую вершину. Поэтому угол 8 = угол 7 = 142°.

Таким образом, все искомые углы будут следующими:
Угол 1 = 142°
Угол 2 = 142°
Угол 3 = 38°
Угол 4 = 38°
Угол 5 = 38°
Угол 6 = 142°
Угол 7 = 142°
Угол 8 = 142°