Изображена правильная треугольная пирамида sabc.отрезок sk - медиана треугольника sbc,точка о - середина отрезка sk.прямая m,лежащая на плоскости грани sbc,проходит через точку о параллельна прямой bc.докажите,что расстояние от точки s до прямой m равно расстоянию между прямыми m и bc.
Другие вопросы по теме Геометрия
Популярные вопросы
- Как вы понимаете выражение торжественная бумага в предложении мать, дедушка...
2 - Осуществите превращения: cl2-kcl-k2so4-kno3-o2-k2o...
1 - 1correct the grammatical mistakes in the. questions. 1 who you did read...
1 - Для детского сада купили 18 мечей за a тг. 1) какова стоимость 27 мечей...
2 - Пять созвездийкоторые которые мне хотелосьбы увидеть...
3 - надо. пункты а , е и f находятся на прямой b. определи длину ae и af...
3 - Звёзды блестят на темном небе чисто и нежно синтаксический разбор...
2 - Масса 3 одинаковых пачек чая 150 г. 1) найди массу 7 таких пачек. 2)сколько...
3 - Начерти прямые a и b пересекающиеся в точке k...
1 - Нужен перевод на и как читается на меня зовут александра, мне 15 лет....
2
Ч.т.д.
Объяснение:
Расстояние от точки до прямой - это длина перпендикуляра, проведённого из данной точки к этой прямой.Так как пирамида правильная, значит её боковые грани представляют собой равнобедренные треугольники.
А это значит, что - равнобедренный.
- равнобедренный.
И по свойству равнобедренного треугольника, - медиана, биссектриса, высота
- медиана, биссектриса, высота  .
.
По условию, - середина
- середина  .
.
Значит .
.
Также по условию,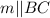 и m ∈ (SBC)
и m ∈ (SBC) 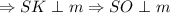 .
.
Значит, расстояние от точки S до прямой m равно расстоянию между прямыми m и BC.