1. Геометрия
  2. Изображен прямоугольный параллелепипед,

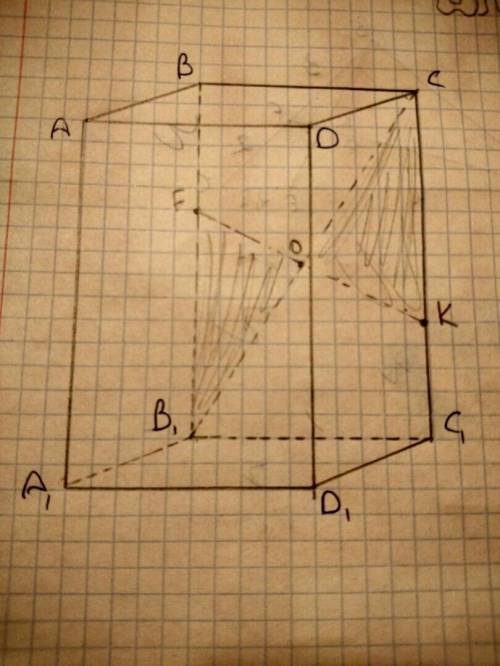
Изображен прямоугольный параллелепипед, точки k и f лежат на ребрах сс1 и bb1 соответственно. прямая сb1 проходит через точку o-середину отрезка kf. докажите, что треугольник kco = треугольнику fb1o

sport22 sport22    1   03.09.2019 14:40    4

Ответы
ник3096 ник3096  06.10.2020 15:06
FO=OK - по условию. B1O=OC - по свойству параллелепипеда (точка пересечения диагонали с линией, вышедшей из ребра параллелепипеда делит диагональ пополам) угол СОК= углу В1ОF - как вертикальные. Соответственно, треугольник B1FO=треугольнику OCK - по двум равным сторонам и углу между ними. Что и требовалось доказать.
Изображен прямоугольный параллелепипед, точки k и f лежат на ребрах сс1 и bb1 соответственно. прямая
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
alisher0901 alisher0901  03.04.2020 00:30
Из точки А к окружности с центром О и радиусом 8 см проведены касательные АВ и АС (В и С – точки касания). Найдите АВ и АС, если ВАС = 60◦ Из точки М к окружности с центром...
natakleymyk natakleymyk  03.04.2020 00:56
У прямокутнику ABCD до диагонали BD проведено перпендикуляри AE I CF. Ведомо шо AE=6cм EF= 9 см . Найдите стороны прямоугольника Умоляю...
ddasha681 ddasha681  03.04.2020 00:35
Площа трикутника 12 см2, а одна із висот трикутника дорівнює 3 см. Знайти сторону трикутника, до якої проведено цю висоту....
natalivkartoyqc3v natalivkartoyqc3v  20.09.2019 17:30
Втреугольнике mnk внутренний угол при вершине м равен 39 градусов, а внутренний угол при вершине k равен 64 градусов. найдите внешний угол при вершине n. заранее ))...
azimova0113 azimova0113  14.01.2020 12:16
15б7 классдано: bc=nkac=mkдоказать: ab||nm...
toniskvortsov1 toniskvortsov1  14.01.2020 12:15
С7 класс: при ришении каждой : 1)указать пары параллельных прямых(отрезков,лучей). 2)указать секущую 3) доказать параллельность прямых(отрезков,лучей) 10 !...
kolkolkim8a2016 kolkolkim8a2016  14.01.2020 11:52
Как древние люди изучали вселенную? кто из учёных доказал что осваивать космос можно с ракеты? когда был запущен первый искусственный спутник земли? можно кратко?...
lehakharitonov lehakharitonov  14.01.2020 11:50
Укажите, какие из утверждений являются верными: - аксиомы доказывают с других аксиом. - теоремы доказывают с аксиом и других теорем. - «через две точки можно провести лишь...
OlesyaSteb OlesyaSteb  14.01.2020 11:47
Найдите стороны равнобедренного треугольника , его p= 30 см,а боковая сторона на 9 см меньше основания...
glushak527 glushak527  01.05.2020 09:36
Найдите площадь кругового сектора, если вписанный угол соответствующий центральному углу сектора,равен 150 градусов, а радиус окружности равен 6 см​...

Популярные вопросы