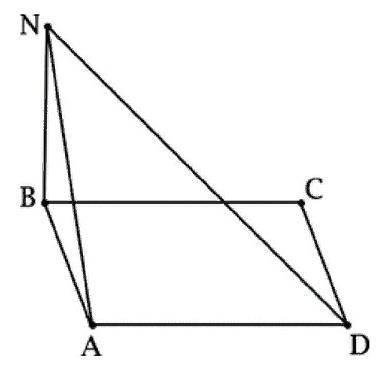
Из точки N на плоскость прямоугольника ABCD опустили перпендикуляр NB. Известно, что AD=7, NA=24. Найдите ND.

Для решения этой задачи мы можем использовать теорему Пифагора и свойства прямоугольников.

Шаг 1: Определение свойств прямоугольника
Прямоугольник ABCD имеет четыре прямых угла, противоположные стороны параллельны и равны друг другу.

Шаг 2: Постановка задачи
Мы должны найти длину отрезка ND.

Шаг 3: Использование теоремы Пифагора
Изображение показывает, что треугольник ADN - прямоугольный треугольник, поскольку перпендикуляр NB опущен из точки N на сторону AD прямоугольника ABCD.

Согласно теореме Пифагора, сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы. Мы можем использовать эту теорему для нахождения ND.

Шаг 4: Запись известных данных
AD = 7
NA = 24

Шаг 5: Нахождение ND
Мы должны найти длину отрезка ND. Пусть ND = x.

Так как треугольник ADN - прямоугольный, мы можем применить теорему Пифагора, чтобы найти значение x.

AD^2 + ND^2 = NA^2

7^2 + x^2 = 24^2

49 + x^2 = 576

x^2 = 576 - 49

x^2 = 527

x = √527

Таким образом, длина отрезка ND равна √527.