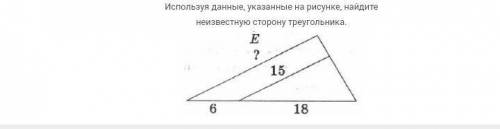
Использую данные на рисунки найдите неизвестные стороны

Для нахождения неизвестных сторон, нам понадобится применить теорему Пифагора. Эта теорема утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В данном случае нам дан прямоугольный треугольник, где известны длины двух сторон (одна катет равна 3 см, а другая равна 4 см) и мы должны найти длину гипотенузы.

Шаг 1: Вспомним формулу для теоремы Пифагора: c^2 = a^2 + b^2, где с - гипотенуза, а и b - катеты.

Шаг 2: Подставим известные значения в формулу: c^2 = 3^2 + 4^2.

Шаг 3: Вычислим квадрат каждого известного значения: c^2 = 9 + 16.

Шаг 4: Сложим полученные значения: c^2 = 25.

Шаг 5: Извлечем квадратный корень из обоих сторон уравнения, чтобы найти длину гипотенузы: c = √25.

Шаг 6: Вычислим корень из 25: c = 5.

Таким образом, неизвестная сторона (гипотенуза) в данном треугольнике равна 5 см.