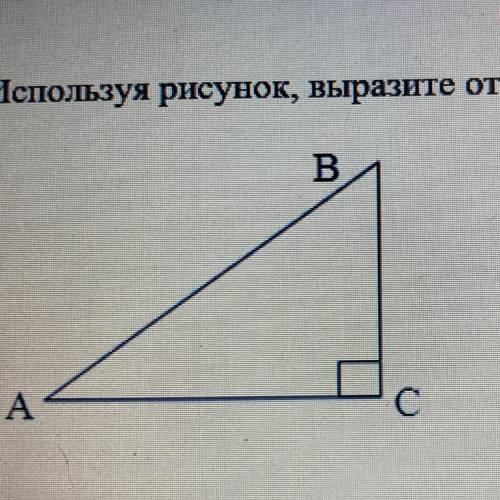
Используя рисунок, выразите отрезoк ВС через тригонометрические функции, если известно, что АВ = 7 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Определить общее сопротивление участка цепи (оформить как решение задачи), изображенного...
2 - Дайте відповідь на питання: «Які загальнолюдські цінності утверджувало християнство?»...
3 - Реши систему уравнений {−0,1k=18 { k+m=−7...
2 - Описать репродукцию картины алексея харламова юные цветочницы...
1 - Тік бұрышты параллелипедтің, текшенің жақтары болып табылатын фигулалады ата...
2 - Внимательно прочитайте приведенный ниже текст и вставьте пропущенные слова:«Если...
3 - Варшава калысында 1 мамыр таңдай...
2 - Какие полезные ископаемые относятся к топливным? (Может быть несколько вариантов...
2 - 1 Use Passive Voice: Present Simple, Past Simple or Present Perfect. Раскройте...
1 - Тема 1. Географическое положение России. 1. Площадь России составляет ( в млн...
3
Теорема косинусов говорит, что в любом треугольнике со сторонами a, b и c и углом α против стороны a, можно выразить одну из его сторон через другие стороны и угол между ними:
c^2 = a^2 + b^2 - 2ab*cos(α)
В нашем случае, если мы обозначим отрезок ВС как с, то сторона AC соответствует стороне a, сторона AB соответствует стороне b, и угол CAB - α.
Из условия известно, что AB = 7 см. Также, в рисунке нам даны значения углов. Угол CAB мы обозначим как α, и в задаче он равен 60°.
Мы хотим выразить отрезок ВС через тригонометрические функции, поэтому нам нужно использовать косинус.
Используя теорему косинусов, получаем:
c^2 = a^2 + b^2 - 2ab*cos(α)
c^2 = AC^2 + AB^2 - 2*AC*AB*cos(CAB)
c^2 = AC^2 + (7 см)^2 - 2*AC*(7 см)*cos(60°)
Теперь нам нужно найти значение AC. Для этого мы можем использовать теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике с катетами a и b и гипотенузой c, квадрат гипотенузы равен сумме квадратов катетов:
c^2 = a^2 + b^2
В нашем случае у нас есть прямоугольный треугольник, и мы знаем, что CD - это высота, поэтому он является катетом. Определим BC как второй катет и AC как гипотенузу:
AC^2 = BC^2 + CD^2
AC^2 = (8 см)^2 + (3 см)^2
AC^2 = 64 см^2 + 9 см^2
AC^2 = 73 см^2
Теперь, подставив значение AC в наше выражение для c^2, получаем:
c^2 = 73 см^2 + (7 см)^2 - 2*(73 см)*(7 см)*cos(60°)
c^2 = 73 см^2 + 49 см^2 - 2*(73 см)*(7 см)*0.5
c^2 = 73 см^2 + 49 см^2 - 511 см
c^2 = 289 см^2
Таким образом, отрезок ВС (c) равен квадратному корню из 289, то есть c = √289 = 17 см.
Ответ: Отрезок ВС равен 17 см.