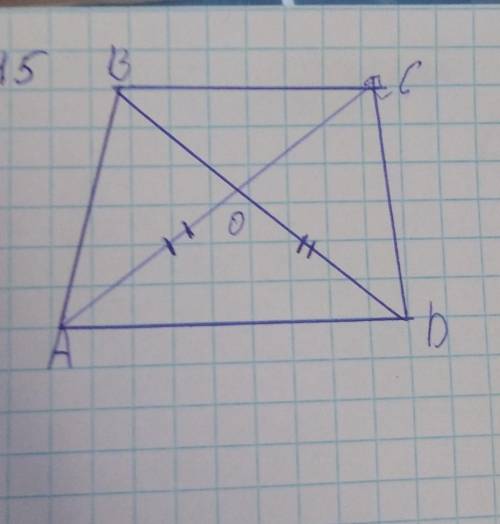
Используя данные рисунка найдите длину OC Если OB=6см​

Для решения этой задачи, нам нужно использовать основные геометрические свойства и формулы.

На рисунке, мы имеем треугольник OBC, где OB является одним из его сторон, а OC - это гипотенуза этого треугольника.

Мы знаем, что OB = 6 см.

Чтобы найти длину OC, нам нужно использовать теорему Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы (OC^2) равен сумме квадратов катетов (OB^2 + BC^2).

Для нашего треугольника, катет BC отсутствует на рисунке, но мы можем найти его, используя теорему Пифагора в другом треугольнике.

Мы замечаем, что треугольник ABC является прямоугольным треугольником с прямым углом в точке B. Поэтому мы можем использовать теорему Пифагора в нем.

Мы знаем, что AB = 8 см и AC = 10 см. Нам нужно найти BC.

Прверим, являются ли стороны треугольника ABC катетами. Для этого проверим соответствие соотношению Пифагора для катетов:

AB^2 + BC^2 = AC^2
8^2 + BC^2 = 10^2
64 + BC^2 = 100
BC^2 = 100 - 64
BC^2 = 36
BC = sqrt(36)
BC = 6 см

Таким образом, мы нашли, что BC = 6 см.

Используем эту информацию, чтобы вернуться к нашей исходной задаче. Теперь, мы можем использовать теорему Пифагора в треугольнике OBC:

OC^2 = OB^2 + BC^2
OC^2 = 6^2 + 6^2
OC^2 = 36 + 36
OC^2 = 72
OC = sqrt(72)
OC = 8.49 см

Таким образом, длина OC равна примерно 8.49 см.