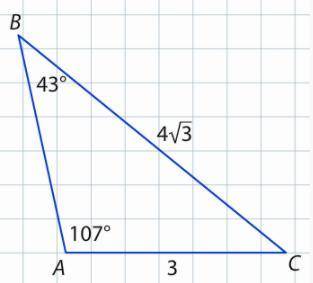
Используя данные рисунка, найдите АВ. ab=43 градуса, a=107 градусов, ac=3см, bc=4√3

Для решения данной задачи, мы можем использовать теорему синусов.

Теорема синусов утверждает, что отношение длины стороны треугольника к синусу противолежащего ей угла равно одинаково для всех трех сторон и углов треугольника.

В данном треугольнике АВС, мы знаем значение угла b - ab = 43 градуса, угла a - a = 107 градусов, длину отрезка ac = 3 см и отрезка bc = 4√3 см.

Теперь мы можем применить теорему синусов для нахождения длины отрезка АВ.

Согласно теореме синусов, мы можем записать следующее соотношение:

AB/sin(b) = BC/sin(a)

Заменяя значения, которые у нас есть, получаем:

AB/sin(43) = (4√3)/sin(107)

Чтобы найти длину отрезка AB, нам нужно избавиться от sin(43) в знаменателе. Мы можем это сделать, умножив обе части равенства на sin(43):

AB = (sin(43) * (4√3))/sin(107)

Теперь мы можем найти значение отрезка AB, выполнив необходимые вычисления:

AB ≈ (0.682,3 * (4 * 1,732))/0.9135

AB ≈ (2,764,6)/0,9135

AB ≈ 3020.883

Значение отрезка AB составляет примерно 3020.883 см.

Вот и весь подробный ответ на задачу.