1. Геометрия
  2. Гипербола, у которой асимптоты

Гипербола, у которой асимптоты являются координатными осями и прямая с уравнением 3x-4y-12=0 является касательной, имеет уравнение: ответ: xy+3=0
Как решить?

Италия13 Италия13    1   17.07.2020 13:18    2

Ответы
MWO MWO  15.10.2020 15:24

Преобразуем уравнение прямой в явный вид

3x-4y-12=0 = -4y=12-3x = y=\frac{3}{4}x-3

Так как асимптотами гиперболы являются координатные оси, ее уравнение можно представить в виде

y=\frac{a}{x} где а - некоторый параметр, его мы и будем искать.

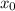Пусть x_0 - точка касания, тогда справедливо следующее

- значение неизвестной функции в точке касания и прямой совпадают

\frac{a}{x_0}=\frac{3}{4}x_0-3

- значение производной в точке касания совпадает с угловым коэффициентом прямой

-\frac{a}{x_0^2}=\frac{3}{4}

Эти два уравнения образуют систему, разрешим ее относительно параметра а

a=-\frac{3}{4}x_0^2

-\frac{3}{4}x_0^2\frac{1}{x_0}=\frac{3}{4} x_0-3

-\frac{3}{4}x_0=\frac{3}{4}x_0-3

-\frac{3}{2}x_0=-3 = x_0=2

Тогда параметр а

a=-\frac{3}{4}*2^2=-3

Значит, уравнение гиперболы имеет вид

y=-\frac{3}{x}

Или, в неявной форме

xy=-3 = xy+3=0

Что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
avysocka avysocka  15.05.2020 17:44
Сторона основания правильной треугольной пирамиды равна 30 м, боковое ребро с плоскостью основания образует угол 30°. Вычисли высоту пирамиды....
nastyabro123 nastyabro123  15.05.2020 17:43
Накресліть за до транспортира кут, градусна міра якогодорівнює 80˚. Побудуйте (без транспортира) кут, що дорівнює даному, і його бісектрису....
zaev1990 zaev1990  15.05.2020 17:43
Точка C - середина відрізка AB.знайдіть координати точки C,якщо A(-3;-2) b(5;-4) будьласка,остані бали(...
TTe4enkaTyan TTe4enkaTyan  06.05.2020 21:09
БУДЬЛАСКА З ПОЯСНЕННЯМ Два кола з центрами в токках О і О1 перетинаються в точках А і В. Доведіть,що трикутники ОАО1 і ОВО1 рівні....
keramix keramix  06.05.2020 21:09
ЗАДАНИЕ В ПРИКРЕПЛЁННОМ ФАЙЛЕ,...
Топирчик Топирчик  06.05.2020 21:10
Середня лінія трапеції дорівнює 12 см, а більша основа - 14 см. Знайдіть меншу основу...
msSisi1 msSisi1  06.05.2020 21:10
Мама біля будинку створює нову квіткову клумбу. Вона хоче, щоб клумба мала форму прямокутника зі сторонами 10 м і 24 м. Щоб перевірити, чи має клумба прямокутну форму,...
Exzampkle Exzampkle  06.05.2020 21:11
Решите систему неравенств-3(x+1)-4 2(х-4)и укажите верный ответ....
bar569 bar569  06.05.2020 21:12
У прямокутному трикутнику МСР кут С=90,MK - бісектриса трикутника, кутCMP=60,Знайдіть довжину катета CP,CK=9см...
ВІДМІННИК11 ВІДМІННИК11  06.05.2020 21:15
Преобразуйте выражение : sin^2(п+а)/sin^2(a-3п/2) - sin^2a+cos^2a/cos^2(a+2п) +1 Варианты ответов : 1) 2-1/cos^2a 2) 2 3) 0 4) 1/cos^2а...

Популярные вопросы