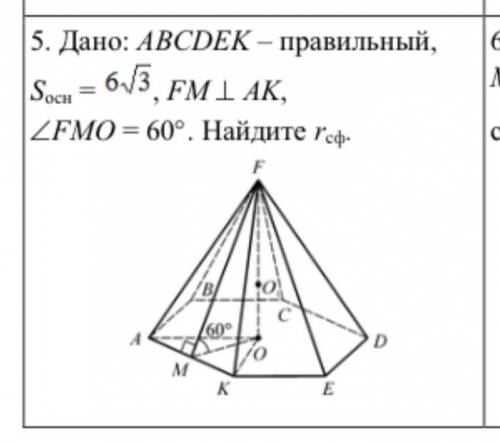
Геометрия. Дано: ABCDEK–правильный, Sосн= 6 корней из 3 , FM перпендикулярно AK, угол FMO= 60 градусов. Найти радиус сферы
Другие вопросы по теме Геометрия
Популярные вопросы
- составьте логическую схему,показывающую последствия уничтожения...
3 - Врезультате чего образуются свободные заряды в вакууме?...
2 - 1.определите тип связи в веществах,дать название им si bacl2 h2...
1 - Мужчина с нормальной пигментацией кожи и толстыми губами вступил...
3 - Вэлектрическом чайнике мощностью 800 вт 2 литра воды нагревается...
1 - Напишите сочинение моя любимая сказка андерсана...
2 - Кто умеет писать сочинения по егэ как расскрывать категории...
3 - Составить предложения 5 или 4 о продавце который продаёт ткани .и...
1 - Найдите точки экстремума функции y=1/3x^3-4x-3...
3 - 4! выполни деление с остатком. 32450÷90 ÷÷÷÷÷2800 составь и реши...
2
do
Из условия задачи мы знаем, что ABCDEK - правильный многогранник, что означает, что все его грани равны и все его углы равны.
Также, нам дано, что Sосн равен 6 корней из 3.
Мы видим на рисунке, что FM перпендикулярно AK и угол FMO равен 60 градусов.
Давайте разберемся сначала со сторонами и углами треугольника FMO.
Так как угол FMO равен 60 градусов, то треугольник FMO является равносторонним. Это означает, что все его стороны равны. Пусть длина каждой стороны равна a.
Теперь давайте рассмотрим треугольник FAK. Мы знаем, что сторона FA также равна a, так как она является стороной равностороннего треугольника FMO. Мы также знаем, что угол FAK равен 90 градусов, так как FM перпендикулярно AK.
По теореме Пифагора, мы можем найти длину стороны AK:
AK^2 = FA^2 + FK^2
Мы знаем, что FA = a и FK = a/2, так как треугольник FAK делится FM на две равные части.
Подставляя значения, получим:
AK^2 = a^2 + (a/2)^2
AK^2 = a^2 + a^2/4
AK^2 = 5a^2/4
С другой стороны, мы знаем, что площадь пятиугольника ABCDE равна Sосн. Площадь правильного пятиугольника можно найти по формуле:
Sосн = (5/4) * a^2 * cot(180°/5)
Cot(180°/5) - это котангенс угла 180°/5. Зная значение площади Sосн, мы можем выразить a:
(5/4) * a^2 * cot(180°/5) = 6√3
a^2 * cot(180°/5) = 24√3/5
a^2 * √5 - a^2 * √5/5 = 24√3/5
a^2 * (√5 - √5/5) = 24√3/5
a^2 * (5√5/5 - √5/5) = 24√3/5
a^2 * (4√5/5) = 24√3/5
a^2 * 4√5 = 24√3
a^2 = 24√3 / 4√5
a^2 = 6√3 / √5
a^2 = 6√15 / 5
Возвращаясь к стороне AK, мы можем подставить полученное значение a:
AK^2 = 5a^2/4
AK^2 = 5 * 6√15 / 5 * 4
AK^2 = 3√15 / 4
Теперь рассмотрим треугольник OAK. Мы знаем, что угол AKO равен 90 градусов, так как OK перпендикулярно AK.
Используя теорему Пифагора, мы можем найти OA:
OA^2 = OK^2 + AK^2
Мы знаем, что OK = Sосн/2 = 6√3/2, так как радиус сферы задан равным Sосн/2.
Подставляя значения, получим:
OA^2 = (6√3/2)^2 + 3√15 / 4
OA^2 = 27/2 + 3√15 / 4
OA^2 = 54/4 + 3√15 / 4
OA^2 = (54 + 3√15) / 4
Итак, радиус сферы равен корню из выражения OA^2:
R = √((54 + 3√15) / 4)
Это и есть окончательный ответ на задачу.