Геометрия 8 класс, нахождение площади фигуры
Решить с формулами и всем остальным



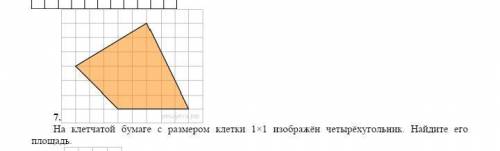
Другие вопросы по теме Геометрия
Популярные вопросы
- Почему Андрей скрывал свой микроскоп от Супруги рассказ микроскоп...
2 - What was necessary to make a young actor look old??ответьте...
3 - Будут ли равны треугольники ACB и DCE если на рисунке 6 :а) A=D, B=E;...
2 - Расставить ударение. Пуховый, типаж, искоса, повторим, шарфы, перезвонит,...
3 - Следуя от озера Эйр-Норт до Сиднея, я видел...продолжите...
2 - Саша поймал шесть карасей. Их длины: 13 см, 10 см, 9 см, 12 см, 11...
2 - Дан текстовый файл. Найти самую короткую строку и ее длину. C++...
3 - Как выразит y через x в уравнении 0.3x + 0.8y = -6...
3 - Put the verbs in brackets into the correct form: gerund or infinitive....
2 - Тато зачекати. Зачекати виступає в ролі додатка чи це складений присудок?...
3
Сначала разобьем фигуру на два прямоугольника и два треугольника. Затем найдем площадь каждой из них и сложим результаты.
1. Посмотрим на первую фигуру, которая представляет собой прямоугольник. У нас даны две стороны прямоугольника - 12 см и 20 см. Формула для нахождения площади прямоугольника: S = a * b, где a и b - длины сторон. Подставляя значения, получаем: S1 = 12 см * 20 см = 240 см².
2. Вторая фигура также представляет собой прямоугольник. Сторона А имеет длину 12 см, а сторона В - 8 см. С использованием той же формулы, находим площадь этого прямоугольника: S2 = 12 см * 8 см = 96 см².
3. Третья фигура - треугольник. Нам известны два его катета - 8 см и 12 см. Площадь треугольника можно найти с помощью формулы: S = (a * b) / 2, где a и b - длины катетов. Подставляем значения: S3 = (8 см * 12 см) / 2 = 48 см².
4. Четвертая фигура - также треугольник, но на этот раз у нас даны длины его основания и высоты. Основание равно 10 см, а высота - 8 см. Считаем площадь: S4 = (10 см * 8 см) / 2 = 40 см².
Теперь сложим площади всех фигур, чтобы получить общую площадь исходной фигуры: S = S1 + S2 + S3 + S4 = 240 см² + 96 см² + 48 см² + 40 см² = 424 см².
Итак, площадь данной фигуры равна 424 квадратным сантиметрам.