Геометрия, 7 класс, 15 б.
1 задание и все
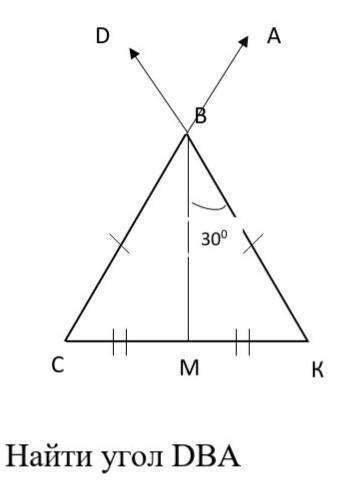
найти угол DBA

180:30=6

6*30=180

Объяснение:

Для решения данной задачи, нам потребуется знание о свойствах углов на прямых и окружностях.

Исходя из вопроса, нам нужно найти угол DBA. Для этого сначала нужно определить зависимые углы, которые имеют одну сторону и лежат между параллельными прямыми.
В данном случае, угол DBA находится между прямыми AC и CE.

Мы видим, что угол DBA образуется хордой DE, которая проходит через центр окружности O. Значит, мы можем использовать свойство треугольника и утверждение, что угол, образованный хордой и касательной окружности, равен половине центрального угла, соответствующего этой же хорде.

Таким образом, чтобы найти угол DBA, нужно найти центральный угол, соответствующий хорде DE, и разделить его на два.

Для нахождения центрального угла, нам нужно определить, как разомкнута дуга DE. В данном случае, мы видим, что эта дуга разомкнута хордой AC. Значит, угол, содержащий данную дугу DE, будет равен половине угла, вершиной которого является точка C, а основаниями - точки A и E.

Из рисунка видно, что угол ACB равен 90 градусам, так как AB - диаметр окружности O, и угол, образованный диаметром и хордой, равен 90 градусам.

Теперь мы можем использовать свойство разностных углов. Угол CBA в данном случае является вертикальным углом к углу ACB. Это значит, что эти углы равны друг другу.

Таким образом, мы можем найти угол CBA, вычитая из 90 градусов угол ACB:
Угол CBA = 90 - 90 = 0 градусов.

Теперь мы можем найти угол DBA, разделив угол CBA на два:
Угол DBA = 0 / 2 = 0 градусов.

Итак, угол DBA равен 0 градусов.