геометрия 7 класс
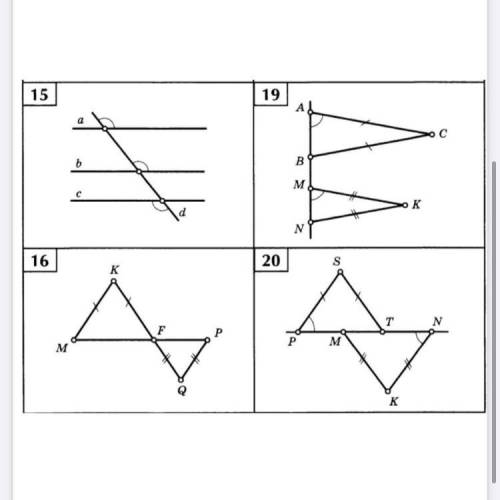
15,16,20

Для решения данной задачи нам необходимо вычислить площадь треугольника.

Сначала, посмотрим на сам треугольник. Он образован сторонами длиной 15 см, 16 см и 20 см.

По свойству треугольника, сумма длин любых двух его сторон должна быть больше, чем длина третьей стороны. В нашем случае, сумма длин сторон 15 и 16 равна 15 + 16 = 31, что больше, чем длина стороны 20. То же самое можно проверить для всех трех комбинаций сторон, поэтому известно, что треугольник с такими сторонами существует.

Чтобы вычислить площадь треугольника, используем формулу Герона:
S = √(p * (p - a) * (p - b) * (p - c))

где S - площадь треугольника, p - полупериметр (p = (a + b + c) / 2), a, b, c - стороны треугольника.

В нашем случае, a = 15, b = 16, c = 20. Подставим значения в формулу:
p = (15 + 16 + 20) / 2 = 51 / 2 = 25.5

S = √(25.5 * (25.5 - 15) * (25.5 - 16) * (25.5 - 20))

Теперь, давайте посчитаем значения внутри квадратного корня:
25.5 * (25.5 - 15) * (25.5 - 16) * (25.5 - 20) = 25.5 * 10.5 * 9.5 * 5.5 = 33857.125

А теперь возьмем квадратный корень из этого значения:
√(33857.125) ≈ 184.65

Ответ: Площадь треугольника со сторонами 15, 16 и 20 равна примерно 184.65 квадратных сантиметров.