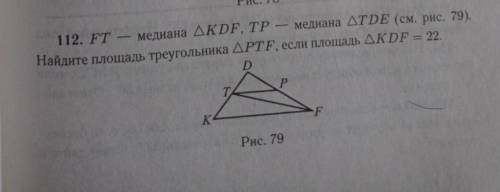
FT - медиана треугольника KDF, TP - медиана треугольника TDE. Найдите площадь треугольника PTF, если площадь треугольника KDF = 22

Добрый день! Давайте решим задачу по нахождению площади треугольника PTF.

Нам дано, что FT - медиана треугольника KDF, а TP - медиана треугольника TDE.

Чтобы решить эту задачу, нам понадобится использовать несколько фактов о медианах треугольников.

1. Факт: Медиана треугольника делит его на две равные по площади части.

Теперь посмотрим на изображение. Мы видим, что медиана FT делит треугольник KDF на две равные по площади части. Давайте обозначим эти части как треугольники AFT и BFT.

Таким образом, площади треугольников KDF и AFT равны, и каждая из них равна половине площади треугольника KDF. Так как площадь треугольника KDF равна 22, то площадь треугольников KDF и AFT равна 22/2 = 11.

2. Факт: Медиана треугольника делит противоположный ей отрезок в отношении 2:1.

Согласно этому факту, линия TP делит отрезок DE в отношении 2:1. Это означает, что длина отрезка DP равна 2/3 длины отрезка DE.

Теперь мы можем перейти к решению задачи.

1. Найдем площадь треугольника BFT:
- Так как FT - медиана треугольника KDF, треугольник BFT - подобен треугольнику KDF.
- Это означает, что отношение длин сторон треугольников KDF и BFT равно 1:1.
- Поэтому площадь треугольника BFT также равна 11.

2. Найдем площадь треугольника TEF:
- Заметим, что треугольники TEF и BFT - подобны и некоторые их стороны пропорциональны.
- Согласно факту о медиане, отрезок DP имеет длину 2/3 от длины отрезка DE.
- Поэтому сторона TF треугольника TEF имеет длину, равную 2/3 стороны FT треугольника BFT.
- Так как сторона FT треугольника BFT равна стороне DF треугольника KDF, а площадь треугольника KDF равна 22, то сторона FT равна корню квадратному из 22.
- Тогда сторона TF равна (2/3) * корень квадратный из 22.
- Так как медиана TP делит сторону DE в отношении 2:1, то сторона TE равна 2/3 стороны DE.
- Так как сторона DE равна стороне DF треугольника KDF, а площадь треугольника KDF равна 22, то сторона DE равна корню квадратному из 22.
- Тогда сторона TE равна (2/3) * корень квадратный из 22.
- Таким образом, площадь треугольника TEF равна (1/2) * TF * TE = (1/2) * ((2/3) * корень квадратный из 22) * ((2/3) * корень квадратный из 22).

3. Найдем площадь треугольника PTF:
- Заметим, что треугольники PTF и TEF - подобны и некоторые их стороны пропорциональны.
- Так как FT - медиана треугольника KDF, то PT - медиана треугольника TDE.
- Согласно факту о медиане, медиана делит треугольник на две равные по площади части.
- Таким образом, площадь треугольника PTF равна половине площади треугольника TEF, то есть (1/2) * [(1/2) * ((2/3) * корень квадратный из 22) * ((2/3) * корень квадратный из 22)].

Теперь можем продолжать вычисления, упростив их:

(1/2) * [(1/2) * ((2/3) * корень квадратный из 22) * ((2/3) * корень квадратный из 22)] = (1/2) * (1/2) * (2/3) * (2/3) * (корень квадратный из 22) * (корень квадратный из 22)
= 1/4 * 4/9 * 22
= 44/36
= 11/9

Таким образом, площадь треугольника PTF равна 11/9.

Надеюсь, я смог объяснить решение задачи понятно и подробно! Если у вас есть еще вопросы, не стесняйтесь задавать.