Если длины сторон треугольника равны 5 см, 4 см, 7 см, то найди длину окружности, описанной около треугольника.

a = 5 см,

b = 4 см,

c = 7 см.

Найти R.

Запишем теорему синусов:

числитель и знаменатель дроби слева последнего равенства домножим на (b·c).

С учётом того, что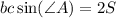 , где S - площадь данного в условии треугольника, имеем

Площадь треугольника можно найти по формуле Герона:

, где

Найдем, сначала, площадь треугольника.

p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.

S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²

Теперь найдем радиус описанной окружности.

R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.

Теперь найдём длину окружности, описанной около данного треугольника.

L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.