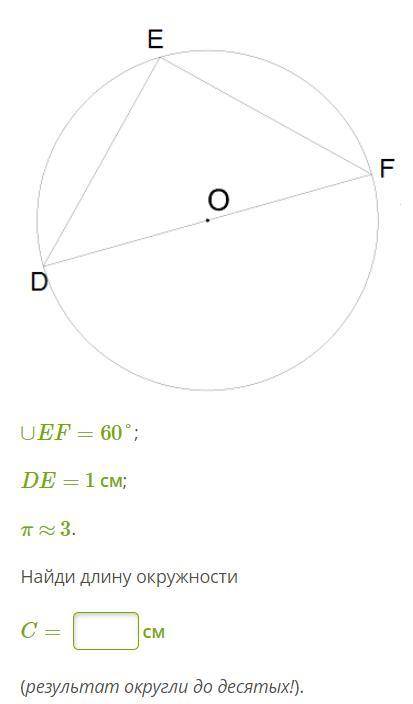
∪EF=60°; DE= 1 см;
π ≈ 3.
∪EF=60°;
DE= 1 см;
π ≈ 3.
Найди длину окружности
С=?
Другие вопросы по теме Геометрия
Популярные вопросы
- Шұғаның белгісі рухани құндылықты попс формуласына салу отыныш...
2 - Обозначте графически условия выбора вставленных орфограмм...
3 - 31 жовтня в Одесі протягом доби були зафіксовані наступні температури -1°,-2°,+4°,+8°,+10°,+7°,+5°,+2°,визначте...
1 - Қожаның әкесінің жақсылығы шағын мәтін. Көмектесіндерш ...
1 - Поясніть, про що свідчать слова Ха-еФа (І.Калинець «Хлопчик- фігурка, який задоволений...
3 - ГРАММАТИКА Завершите предложения глаголами в квадратных скобках с простой формой...
2 - Hassen richtigneuin• in der KlasseEs geht.falschneindas SchulfachaberGeografieNa...
2 - Составить текст из 5 предложений со словами категории состояния....
2 - Русский язык страница 154 упражнение 263 написали Л.М.Бреусенко Т.А.Матохина...
2 - Превили в десятичную дробь обыкновенной ...
2
Формула для вычисления длины окружности (С) радиусом (r) выглядит следующим образом:
С = 2πr,
где π - это число пи, которое примерно равно 3.
В данной задаче нам дан радиус окружности и угол (∪EF), поэтому мы можем использовать эту информацию и формулу для вычисления длины окружности.
Длина окружности (С) вычисляется следующим образом:
С = 2πr,
где r - радиус окружности.
Дано, что DE = 1 см. Нам нужно найти длину окружности (С).
У нас нет явного значения радиуса в этой задаче, но мы можем использовать информацию об угле (∪EF), чтобы найти радиус окружности.
В треугольнике DEF, ∪DEF является прямым углом, так как угол (∪EF) равен 60°.
Теперь мы можем использовать теорему синусов, чтобы найти радиус окружности.
Вспомним, что в треугольнике DEF, синус угла (∪DEF) равен отношению противолежащего катета (DE) к гипотенузе (r):
sin(∪DEF) = DE / r.
Мы знаем значение DE (1 см) и можем найти sin(∪DEF) следующим образом:
sin(∪DEF) = DE / r,
sin(60°) = 1 / r.
Так как sin(60°) = √3 / 2, мы можем записать уравнение:
√3 / 2 = 1 / r.
Теперь мы можем решить это уравнение относительно r:
2 / √3 = r.
Сокращаем дробь:
2√3 / 3 = r.
Теперь мы знаем значение радиуса (r), которое равно 2√3 / 3 см.
Теперь мы можем использовать это значение радиуса в формуле для вычисления длины окружности:
С = 2πr.
Подставляем значение радиуса:
С = 2π(2√3 / 3).
Упрощаем выражение:
С = 4π√3 / 3.
Таким образом, длина окружности (С) равна 4π√3 / 3 см.