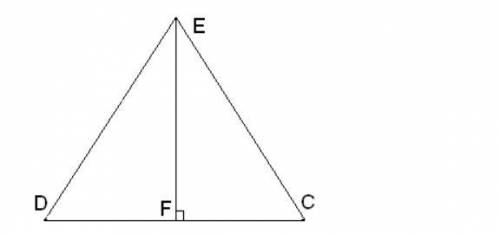
EC=ED,∢CED=31°.

Угол DEF равен

°.

Объяснение:

63.5

Для решения данной задачи нам понадобится использовать свойство углов треугольника и факт возможности расчета неизвестных углов с помощью их суммы.

Первым шагом посмотрим на данные задачи. У нас дано, что отрезок EC равен отрезку ED (EC=ED) и у нас есть значение угла CED (∢CED=31°). Нам нужно найти значение угла DEF.

Давайте начнем, сравнивая две равные стороны треугольника. Отрезок EC равен отрезку ED. Если у нас есть две равные стороны треугольника, это указывает, что углы напротив этих сторон также равны.

Таким образом, угол CDE должен быть равен углу CED. Угол CDE равен 31°, поэтому и угол CED также равен 31°.

Теперь мы можем использовать свойство суммы углов треугольника. Сумма углов треугольника всегда равна 180°.

Мы знаем, что угол CED равен 31°, поэтому мы можем записать следующее уравнение:

CED + DEF + EDF = 180°

Мы уже знаем, что CED = 31°, поэтому мы можем подставить это значение в уравнение:

31° + DEF + EDF = 180°

Теперь нам нужно найти значение для угла DEF. Для этого нам нужно избавиться от EDF.

Мы также знаем, что отрезок EC равен отрезку ED. Это также означает, что угол EDC равен углу ECD.

Таким образом, угол EDC равен 31°. Но сумма углов треугольника также равна 180°, поэтому мы можем записать еще одно уравнение:

EDC + ECD + EDC = 180°

31° + ECD + 31° = 180°

Теперь нам нужно найти значение для угла ECD. Чтобы избавиться от EDC, мы знаем, что EDC равен ECD + EDC.

Таким образом, ECD + ECD + 31° = 180°

2ECD + 31° = 180°

2ECD = 180° - 31°

2ECD = 149°

ECD = 149° / 2

ECD = 74,5°

Теперь у нас есть значение для угла ECD, которое равно 74,5°. Мы можем использовать это значение, чтобы найти значение для угла DEF.

Воспользуемся нашим первоначальным уравнением:

31° + DEF + EDF = 180°

31° + DEF + 74,5° = 180°

DEF = 180° - 31° - 74,5°

DEF = 180° - 105,5°

DEF = 74,5°

Таким образом, угол DEF равен 74,5°.