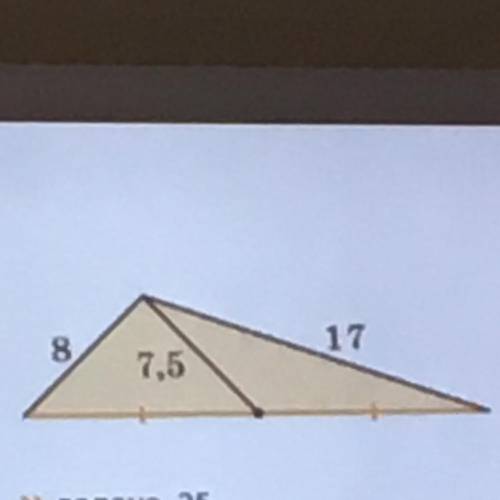
Две стороны треугольника равны 8 и 17, а медиана, проведённая к третьей 7,5. Найдите площадь треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Камень массой = 0,4 кг падает из состояния покоя с высоты = 10 м. определите,...
1 - К100 г 30% раствора добавлено 800 мл воды. определить процентную концентрацию...
3 - Какая страна австрии подавить венгерское восстание в 1849 г. а. пруссия б....
3 - Вкатушке с 150 витками провода течет ток 7.5 а. при этому создается магнитный...
3 - Кдоядерным (прокариотическим) относятся: а) вирусы б) бактерии и сине-зелёные...
3 - На движущийся мотоцикл массой 500 кг в горизонтальном направлении действует...
2 - Задайте общий,альтернаиивный и специальный вопросы: 1.ann is a student. 2....
2 - Put the verbs in the correct tense: 1. i (think) he s away. 2. you (know)...
1 - Добери до iншомовних слiв украiнськi вiдповiдники.слова запиши парами.екзамен...
1 - Ялюблю смотреть телевизор ! подлежащие и сказуемое в этом предложении ?...
2
S = (1/2) * a * b * sin(C)
где S - площадь треугольника, a и b - длины двух сторон треугольника, C - угол между этими сторонами.
Так как в задаче даны только две стороны и медиана, нам необходимо найти угол С.
Сначала давайте найдем третью сторону треугольника. По условию задачи, одна сторона равна 8, а вторая сторона равна 17. Пусть третья сторона будет с.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти третью сторону:
a^2 + b^2 = c^2
8^2 + 17^2 = c^2
64 + 289 = c^2
353 = c^2
c = √353
Теперь, чтобы найти угол С, мы можем воспользоваться теоремой косинусов, которая гласит:
c^2 = a^2 + b^2 - 2ab * cos(C)
В нашем случае, c = √353, a = 8, b = 17. Подставим значения:
√353^2 = 8^2 + 17^2 - 2 * 8 * 17 * cos(C)
353 = 64 + 289 - 272cos(C)
353 = 353 - 272cos(C)
-272cos(C) = 0
cos(C) = 0
Так как косинус равен нулю, значит, угол С равен 90 градусов.
Теперь, имея длины сторон и угол, мы можем найти площадь треугольника:
S = (1/2) * a * b * sin(C)
S = (1/2) * 8 * 17 * sin(90)
S = (1/2) * 8 * 17 * 1
S = 68
Таким образом, площадь треугольника равна 68 квадратным единицам.