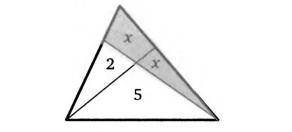
Две прямые делят треугольник на три треугольника и четы­ рехугольник. Площади двух треугольников на рисунке равны 2 и 5.
Найдите площадь четырехугольника, если он равновелик третьему
треугольнику.​

Чтобы найти площадь четырехугольника, мы можем использовать следующую методику:

1. Обозначим площади треугольников на рисунке как S1, S2 и S3, где S1 = 2 и S2 = 5.

2. Разделим четырехугольник на два треугольника, обозначим их площади как S4 и S5. Так как четырехугольник равновелик третьему треугольнику, то мы знаем, что S4 + S5 = S3.

3. Обозначим площадь большего треугольника, который тоже равен S3, как S6.

4. Теперь мы можем записать уравнение, связывающее площади всех треугольников: S1 + S2 + S4 + S5 = S6. Заменяя известные значения площадей S1 и S2, получаем уравнение 2 + 5 + S4 + S5 = S6.

5. Так как S4 + S5 = S3, мы можем заменить S4 + S5 на S3 в уравнении: 2 + 5 + S3 = S6.

6. Теперь мы знаем, что S6 = 2 + 5 + S3.

7. Заметим, что больший треугольник S6 включает маленький треугольник S3. Значит, S6 можно представить как сумму площадей S3 и маленького четырехугольника внутри S6. Обозначим площадь маленького четырехугольника как S7.

8. Теперь мы можем записать уравнение, связывающее площади маленького четырехугольника и треугольников: S7 + S3 = S6. Заменяем известные значения S6 и S7, получаем уравнение S7 + S3 = 2 + 5 + S3.

9. После упрощения получаем уравнение S7 = 7.

Таким образом, мы находим, что площадь маленького четырехугольника равна 7.

Обратите внимание, что местоположение и форма прямых, которые делят треугольник, не имеют значения в данной задаче. Мы только используем информацию о площадях треугольников и равновеликости четырехугольника с одним из треугольников.