Две параллельные плоскости , находящиеся на растоянии 8 друг от друга, пересекают шар. получившиеся

Question

Геометрия: Две параллельные плоскости , находящиеся на растоянии 8 друг от друга, пересекают шар. получившиеся сечения одинаковы, и площадь каждого из них равна 9π. найдите площадь поверхности шара. с рисунком ответ: 20π

hopelless2124 · Answer

1. Очевидно, что если сечения шара плоскостью равны, то он отстоят от центра шара на одинаковом расстоянии. Отсюда мы можем найти расстояние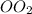 $OO_{2}$ от центра шара до центра круга сечения.

2. Найдем радиус круга в сечении. Из формулы площади круга выражаем радиус.

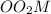3. Рассмотрим прямоугольный треугольник $OO_{2}M$ . В нем угол 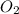$O_{2}$ прямой, поэтому OM (а это радиус шара, который необходим для того, чтобы найти площадь его поверхности) - это гипотенуза. Из теоремы Пифагора находим радиус шара.

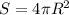4. Площадь поверхности шара: $S=4\pi R^{2}$ . Подставляем найденный чуть выше радиус вместо R и получаем ответ.

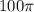
ответ: $100\pi$

Популярные вопросы