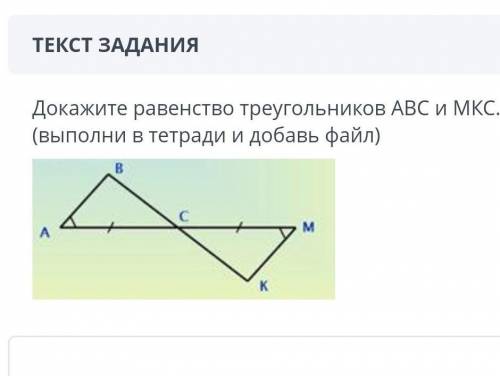
Докажите равенство треугольников ABC и МКС

вот ответ вот ответ

Объяснение:

ну я там прост соч делал как ты заметишь ;ь

Для того чтобы доказать равенство треугольников ABC и МКС, мы должны сравнить их стороны и углы и убедиться, что они совпадают.

По изображению видно, что у треугольников есть общая сторона AC. Также, из рисунка ясно, что угол ABC равен углу МКС. Это можно обозначить следующим образом: ∠ABC = ∠МКС.

Теперь посмотрим на другие стороны и углы треугольников:

1. Сторона AB в треугольнике ABC сопряжена со стороной МК в треугольнике МКС.
2. Сторона BC в треугольнике ABC сопряжена со стороной КС в треугольнике МКС.

Также, мы можем выделить следующие углы:
3. ∠ACB в треугольнике ABC сопряжен с ∠MKC в треугольнике МКС.

На данный момент у нас есть две пары углов и одна пара сторон, которые сопряжены в треугольниках ABC и МКС. Это предоставляет нам информацию о равенстве углов и сторон в этих двух треугольниках.

Чтобы полностью доказать равенство треугольников ABC и МКС, мы должны продемонстрировать, что третья пара сторон и углов также равны.

Мы знаем, что сторона AC общая для обоих треугольников, следовательно, она равна сама себе.

Осталось проверить пару углов ∠CAB и ∠MКА.

У нас есть информация, что у треугольников есть общий угол ∠ABC = ∠МКС. Также, мы знаем, что сумма углов в треугольнике равна 180 градусам, поэтому ∠CAB + ∠ACB + ∠ABC = 180 градусов.

Подставим значения, которые мы узнали из предыдущего анализа:
∠MKA + ∠КMС + ∠МКS = 180 градусов.

Комбинируя эти два уравнения, получаем:
∠CAB + ∠MKС + ∠MKA + ∠КMС + ∠МКS = 180 градусов.

Заметим, что ∠MKA и ∠МКS одинаковы, следовательно, мы можем записать:
∠CAB + ∠MKС + ∠КMС + ∠MKA = 180 градусов.

Учитывая факт, что ∠ABC = ∠МКС, мы можем заменить их в уравнении:
∠CAB + ∠ABC + ∠КMС + ∠MKA = 180 градусов.

Теперь мы видим, что у нас есть две пары углов, которые мы могли сравнить:
∠CAB сравниваем с ∠MКА
∠КMС сравниваем с ∠МКS

Мы установили ранее, что ∠ABC равно ∠МКС и это означает, что ∠CAB равно ∠MКА. Также, мы предполагаем, что ∠КMС равно ∠МКS.

Таким образом, мы доказали, что стороны и углы треугольников ABC и МКС совпадают, что означает, что треугольники ABC и МКС равны.