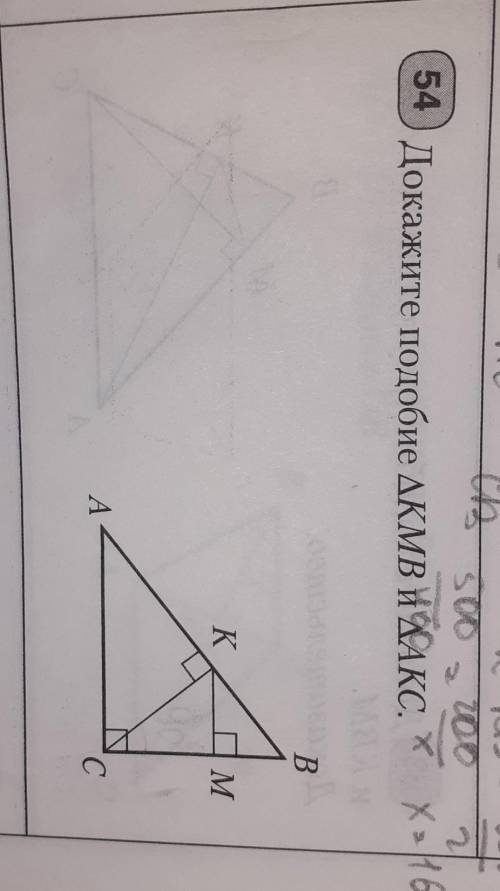
Докажите подобие треугольника KMB и треугольника AKC
полный ответ
Другие вопросы по теме Геометрия
Популярные вопросы
- Чему равна масса латунной детали, если при передачи ей 760 кДж...
3 - Что сохранилось в культуре и образовании от античности?...
1 - Точка О лежит на стороне АВ четырёхугольника АХУВ, причём АО :...
2 - Як князь аскольд відноситься до киянин...
1 - 11. Порівняйте циркуляцію атмосфери в екваторіальних і тропічних...
2 - (10) 3.А)Расставьте вулканы Евразни в порядке расположення в направлении...
1 - Дурыс жауабын там.Айдана хатында не туралыжазды.калын ормандар...
1 - Решить треугольник: А) ∠А = 74°, ∠С = 39°, АВ = 12смБ) АС = 7см,...
2 - русский язык и литература билим Ленд. Варианты: Родины. Степи....
2 - Бүркіттің омыртқасы болама? ...
2
1. Докажем угловое подобие:
- Рассмотрим углы.
- Угол KMB равен углу KAC, так как это вертикальные углы (вертикальные углы равны).
- Углы KMB и KAB являются соответственными углами, так как они лежат на параллельных прямых BM и AC, пересеченных прямой KA.
- Таким образом, углы KMB и KAB равны.
- Углы KAC и KAB также являются соответственными углами, так как они лежат на параллельных прямых BM и AC, пересеченных прямой KA.
- Следовательно, углы KAC и KAB равны.
- Итак, угловое подобие выполняется, так как все углы треугольника KMB равны соответствующим углам треугольника AKC.
2. Докажем соответственность сторон:
- Для этого рассмотрим отрезки BM и AC.
- Отрезок BM является боковой стороной треугольника KMB.
- Отрезок AC является боковой стороной треугольника AKC.
- Длина отрезка BM равна длине отрезка AC, так как BM и AC являются параллельными отрезками (по условию задачи).
- Другая боковая сторона треугольника KMB - отрезок BK.
- Другая боковая сторона треугольника AKC - отрезок AK.
- Отрезки BK и AK являются основаниями высот в треугольниках KMB и AKC соответственно.
- Высоты треугольников имеют общий конец - точку K.
- Таким образом, отрезки BK и AK - это стороны треугольников KMB и AKC, имеющие общий конец K.
- Согласно определению подобных треугольников, соответствующие стороны пропорциональны.
- В данном случае, отрезки BK и AK имеют общую пропорцию с отношением BK/AK = BM/AC, так как стороны треугольников KMB и AKC пропорциональны.
- Таким образом, стороны треугольников KMB и AKC соответственны.
Итак, мы доказали, что треугольник KMB подобен треугольнику AKC.