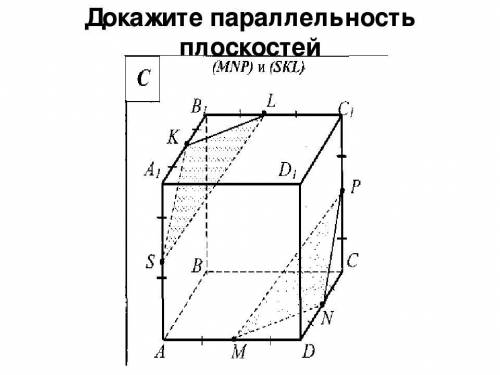
Докажите параллельность плоскостей MNP и skl
Другие вопросы по теме Геометрия
Популярные вопросы
- Если в варёном яйце желток свернулся, а белок нет, значит, яйцо...
1 - Вчём особенность наречие как часть речи...
2 - ответь на вопросы на did you have eggs for breakfast yesterday...
2 - Три сложных предложения на тему природа погода или на новый год...
3 - Нужно написать немножко про кекс(какой он,рассказать про него) на...
1 - 3вопроса про своё любимое блюдо на козаском языке...
3 - Написать ! тарас бульба в запорожской сечи...
2 - Сочиненике на тему кот и кошка и котята...
2 - Сумма двух чисел = 12 целых 4.одно из них в 1 целую 2 раза больше...
3 - Разработайте и заполните сравнительную таблицу отражающую взгляды...
3
Чтобы доказать, что плоскости MNP и skl параллельны, мы должны установить, что их нормали (векторы, перпендикулярные плоскости и задающие их направление) параллельны друг другу.
1. Найдем нормали для каждой плоскости:
Нормаль плоскости MNP: MN x MP, где x обозначает векторное произведение.
MN = (1, 0, -2)
MP = (0, 1, -1)
Выполняем векторное произведение:
MN x MP = ((0 * (-1)) - ((-2) * 1), ((-2) * 0) - (1 * (-1)), (1 * 1) - (0 * 0))
MN x MP = (2, 1, 1)
Нормаль плоскости skl: sk x sl
sk = (-1, 2, 1)
sl = (-2, 1, 1)
Выполняем векторное произведение:
sk x sl = ((2 * 1) - (1 * 1), ((-1) * 1) - ((-2) * 1), ((-1) * 1) - ((-2) * 2))
sk x sl = (1, 1, -3)
2. Проверим, параллельны ли найденные нормали:
Для этого используем определение параллельности векторов - если векторы параллельны, то их координатные отношения равны.
Давайте сравним координатные отношения нормалей:
Координатные отношения нормали плоскости MNP: 2:1:1
Координатные отношения нормали плоскости skl: 1:1:-3
Мы видим, что координатные отношения нормалей различны, а значит, нормали и плоскости не параллельны.
Таким образом, мы доказали, что плоскости MNP и skl не параллельны.