Докажите что в равнобочной трапеции с перпендикулярными диагоналями средняя линия равна высоте
Ответы
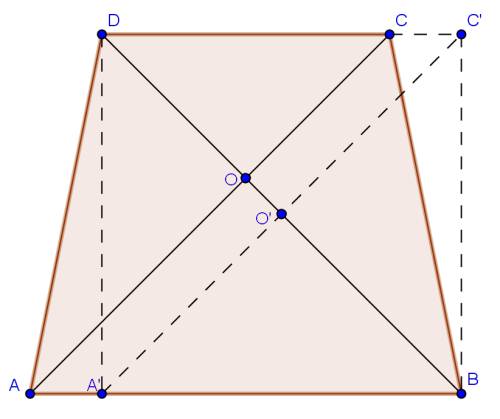
С параллельного переноса вдоль оснований трапеций сдвинем AC так, чтобы угол DC'B стал прямым. При этом сумма "оснований" не меняется, т.к. AA' = CC'; с очевидностью не меняется и высота (=расстояние между параллельными прямыми). Получившийся четырехугольник A'BC'D - квадрат (доказать это можно, например, так: треугольники ADA' и CBC' равны (AB = BC, AA' = CC', BCC' = ADD'), тогда угол BA'D прямой, тогда A'BC'D - прямоугольник, т.к. диагонали перпендикулярны, то квадрат). Но для квадрата утверждение задачи очевидно.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Частица массой заряд q=1,6*10^-19кл,влетает в магнитное поле с индукцией...
3 - Заводское здание состоит из 2х корпусов. вероятность попадения одной...
2 - Шарик массой m=0.6 кг на нерастяжимой нити отклоняют на угол 90°...
2 - Найдите первообразную функции: , график которой проходит через начало...
2 - Найдите промежутки убывания функции f (x)=x^3-2x^2+x...
2 - Ящик фруктов весит 250 кг его тянет тягач со скоростью 25 m/s² какая...
2 - Вычислите: 5 корень 2^5 x 7^2 x 5 корень 7^3...
1 - Вычислите производную функции y=2x/4-x...
3 - Ящик фруктов весит 250 кг его тянет тягач с ускорением 25 m/s² какая...
3 - Кграфику функции y=x^2+3x+2 в точке с абсциссой x=0 проведена касательная....
2