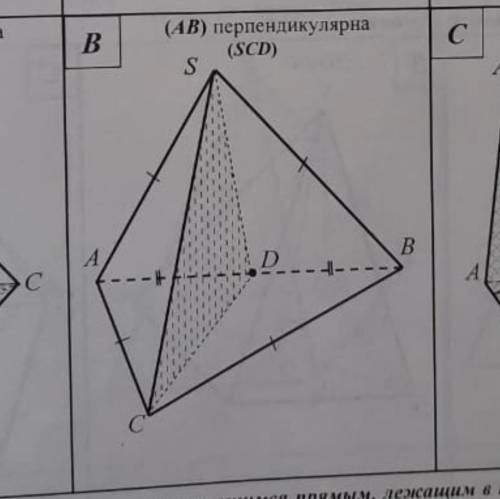
Докажите, что прямая АВ перпендикулярна плоскости (SCD)
Я НЕ ПОНИМАЮ

Для доказательства того, что прямая АВ перпендикулярна плоскости SCD, нам необходимо применить теорему о перпендикулярности прямой и плоскости.

Во-первых, давайте разберемся, что значит, что прямая АВ перпендикулярна плоскости SCD. Перпендикулярность означает, что прямая и плоскость пересекаются под прямым углом, то есть угол между прямой и плоскостью равен 90 градусам.

Для доказательства перпендикулярности прямой и плоскости, обычно используют два способа: через векторное произведение и через свойства векторов.

Давайте рассмотрим оба способа доказательства.

1. Через векторное произведение:
Векторное произведение двух векторов равно вектору, перпендикулярному плоскости, образованной этими векторами. Мы можем воспользоваться этим свойством, чтобы доказать перпендикулярность прямой и плоскости.

Для этого нам понадобятся координаты векторов АВ и SCD.

Вектор АВ можно вычислить, вычтя координаты точки А из координат точки В:
АВ = (x_B - x_A, y_B - y_A, z_B - z_A),

где (x_A, y_A, z_A) и (x_B, y_B, z_B) - координаты точек А и В соответственно.

Теперь нам понадобятся координаты вектора SCD. Видя по рисунку, мы видим, что вектор SCD проходит через точки S и С. Из рисунка мы не видим точки D, но всегда можем найти координаты этой точки, используя данные о координатах С и уравнение плоскости.

В уравнении плоскости у нас есть значения A, B и C, которые определяют нормальный вектор, перпендикулярный плоскости. Вектор нормали к плоскости равен (A, B, C).

Таким образом, вектор SCD можно записать в виде:
SCD = (x_D - x_S, y_D - y_S, z_D - z_S) = (A, B, C),

где (x_D, y_D, z_D) и (x_S, y_S, z_S) - координаты точек D и S соответственно, а (A, B, C) - значения из уравнения плоскости.

Если векторное произведение векторов АВ и SCD равно нулевому вектору, то это означает, что они коллинеарны (или параллельны). И если они коллинеарны, то прямая АВ перпендикулярна плоскости SCD.

2. Через свойства векторов:
Есть свойство, что вектор, лежащий в плоскости и перпендикулярный к нормальному вектору этой плоскости, перпендикулярен самой плоскости.

Если мы можем доказать, что вектор АВ лежит в плоскости SCD и перпендикулярен вектору (A, B, C), то мы докажем, что прямая АВ перпендикулярна плоскости SCD.

Для этого нам снова понадобятся координаты точек А, В и С, а также значения A, B и C из уравнения плоскости.

Преобразуем уравнение плоскости так, чтобы оно имело вид Ax + By + Cz + D = 0. Тогда, нормальный вектор плоскости будет равен (A, B, C).

Теперь мы можем найти векторное произведение векторов АВ и (A, B, C). Если это произведение равно нулевому вектору, то это означает, что они коллинеарны и прямая АВ перпендикулярна плоскости SCD.

Таким образом, мы можем доказать, что прямая АВ перпендикулярна плоскости SCD, применяя теорему о перпендикулярности прямой и плоскости и используя либо векторное произведение, либо свойства векторов.