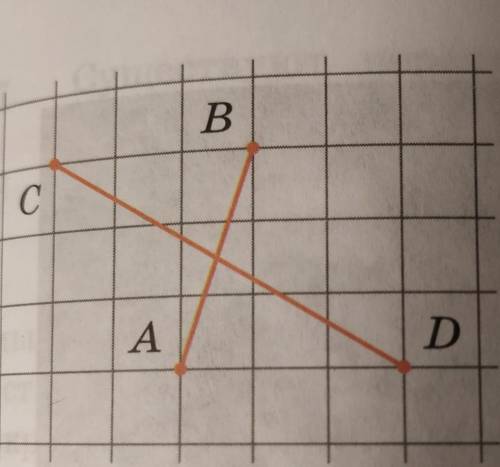
Докажите что отрезки АВ и СD на клетчатой бумаге делятся точкой пересечения пополам
Другие вопросы по теме Геометрия
Популярные вопросы
- Значение выражения а-2/24равно нулю если а=...
2 - проверять через 10 минутЗапишите раскрывая скобки. Выделите окончания в...
2 - Айгуль салфетку размерами 5см*5см разрезала на 2части. найдите периметр...
1 - Сенс пісні Кузьми Скрябіна «Країна»?...
2 - Укажіть кординати точки перетину графіка функції y=-2×+4 з віссю кординат...
1 - Автобус і вантажна машина, швидкість якої на 18 км/год більша від швидкості...
2 - Чому Клим Джура не міг назвати пані Соломію бабусею...
3 - Почему знание своей группы крови может быть для человека жизненно важным?...
1 - Знайдіть косинус кута між векторами а(4:-1) і b(-6;-8)...
2 - Question tags Pokemon Cards are Fun to collect И что дальше...
1
Предположим, что точка пересечения отрезков АВ и СD называется E. Чтобы доказать, что E делит оба отрезка пополам, нам нужно показать, что длина отрезка AE равна длине отрезка EB, а также что длина отрезка CE равна длине отрезка ED.
Давайте разберемся пошагово:
1. Взгляните на изображение и обратите внимание на клетки. Каждая горизонтальная и вертикальная линия на клетчатой бумаге делит ее на одинаковые отрезки. Это значит, что каждая клеточка имеет одинаковую ширину и высоту.
2. Начнем с доказательства, что отрезки AE и EB равны в длине. Разделите отрезок AB и точку пересечения E на 2 половины, обозначив их F и G соответственно. Это означает, что отрезок AF будет равен отрезку FB, и отрезок AG будет равен отрезку GB.
3. Посмотрите на вертикальные отрезки CF и EG. Заметим, что эти отрезки проходят через одни и те же точки решетки, поэтому они имеют одинаковую длину.
4. Проанализируйте горизонтальные отрезки AE и EB. Они также проходят через одни и те же точки решетки, поэтому они имеют одинаковую длину.
Таким образом, мы доказали, что отрезки AE и EB равны в длине.
5. Теперь рассмотрим отрезки CE и ED. Аналогично, разделим отрезок CD и точку пересечения E на 2 половины, обозначив их H и I соответственно. Опять же, отрезок CH будет равен отрезку HD, и отрезок CI будет равен отрезку ID.
6. Посмотрите на вертикальный отрезок CH и горизонтальный отрезок CE. Они пересекаются в точке C, которая является одной из точек решетки. Поэтому отрезок CH имеет то же самое расстояние, что и отрезок CE.
7. Аналогично, рассмотрите вертикальный отрезок DI и горизонтальный отрезок ED. Они пересекаются в точке D решетки, поэтому отрезок DI имеет такое же расстояние, что и отрезок ED.
Таким образом, мы доказали, что отрезки CE и ED также равны в длине.
Таким образом, мы доказали, что отрезки АВ и СD делятся точкой пересечения E пополам.