1. Геометрия
  2. Докажите что а(8; -3) в(2,5)

Докажите что а(8; -3) в(2,5) с(10; 11) д(16,3) является вершинами параллелограмма

donatas6969 donatas6969    2   14.06.2019 05:30    3

Ответы
Danila1367 Danila1367  10.07.2020 22:19
Докажем, что соответствующие вектора, построенные на сторонах параллелограмма, параллельны и их длины равны.

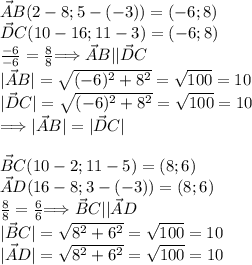
\vec AB(2-8;5-(-3))=(-6;8)\\ \vec DC(10-16;11-3)=(-6;8)\\ \frac{-6}{-6}=\frac{8}{8}$\stackrel{}{\Longrightarrow} \vec AB ||\vec DC \\ |\vec AB|=\sqrt{(-6)^2+8^2}=\sqrt{100}=10\\|\vec DC|= \sqrt{(-6)^2+8^2}= \sqrt{100}=10 \\ $\stackrel{}{\Longrightarrow} |\vec AB|=|\vec DC|\\ \\ \vec BC(10-2;11-5)=(8;6) \\ \vec AD(16-8;3-(-3))=(8;6)\\ \frac{8}{8}=\frac{6}{6}$\stackrel{}{\Longrightarrow}\vec BC||\vec AD\\|\vec BC|=\sqrt{8^2+6^2}=\sqrt{100}=10\\|\vec AD|= \sqrt{8^2+6^2}=\sqrt{100}=10\\
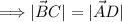
$\stackrel{}{\Longrightarrow}|\vec BC|=|\vec AD|

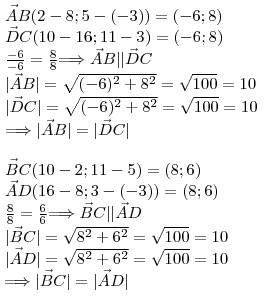
Докажите что а(8; -3) в(2,5) с(10; 11) д(16,3) является вершинами параллелограмма
ПОКАЗАТЬ ОТВЕТЫ
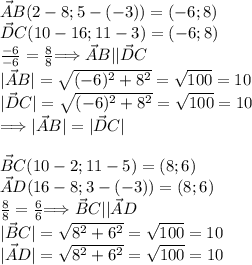
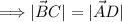
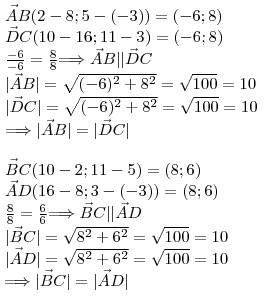
Другие вопросы по теме Геометрия
vgorelova62 vgorelova62  14.04.2020 19:19
Висота циліндра дорівнює H, а осьовий переріз циліндра є квадратом. Знайдіть об єм циліндра. Решите с рисунком и объяснением...
малая188 малая188  14.04.2020 19:19
Одна зі сторін трикутника дорівнює 7 см а дві інші утворюють кут 60°, а їх різниця дорівнює 3 см. Знайдіть площу трикутника.​...
2156kolllokir 2156kolllokir  14.04.2020 19:19
Напишите уравнение прямой, проходящей через точки А(-1;1) И и(1;0)...
Арти2004 Арти2004  14.04.2020 19:19
В четырехугольник ABCD вписана окружность радиусом 1.7 см. Известно, что AB : CD = 2:3, AD: BC = 2:1. Найдите стороны четырехугольника, если его площадь равна 12.75...
darina2605 darina2605  14.04.2020 19:19
От точки C на окружности хорда AB видна под углом 82° . Вычисли градусную меру дуги AB и дуги ACB....
Простоелена26 Простоелена26  25.03.2021 17:36
На дiагоналi квадрата як на сторонi побудовано iнший квадрат. Доведiть, що його площа вдвiчi бiльша за площу даного квадрата...
Этотникужезанят146 Этотникужезанят146  25.03.2021 17:37
У трикутнику АВС проведені висоти АЕ і СД, що перетинаються в точці О. Знайти кут АОС, якщо кут В - 60 градусів....
игорь800 игорь800  25.03.2021 17:37
Определи величины углов равнобедренного треугольника DLG, если внешний угол угла D при основании DG равен 146°. ∡D=∡L=∡G=...
ANT1XA1P ANT1XA1P  25.03.2021 17:38
В прямоугольном треугольнике проведена высота к гипотенузе. Какие углы эта высота образует с катетами, если больший из острых углов этого треугольника равен 64°? 1....
fg4ne fg4ne  25.03.2021 17:41
Дано: ∢MLK=54°. Данный угол является углом треугольника MLK.Укажи вид треугольника MLK:тупоугольныйневозможно определитьостроугольныйпрямоугольный​скажите мне...

Популярные вопросы