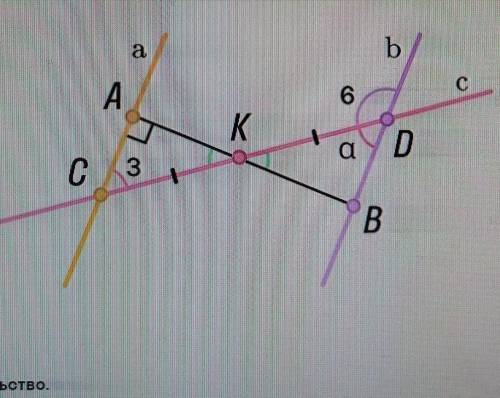
Доказательство. 1.<3 - <6 = 180° (по условию), а <KDB + <6 = 180° (как смежные), следовательно, <3 = <KDB.
2 <СКА = <... (как вертикальные углы), <3 = <KDB = а, CR=... значит, треугольник СКА = треугольник... по (... ). 3 Если треугольник СКА прямоугольный, то и дDKB прямоугольный, и AB перпендикулярен к прямой b. 4 По первому признаку прямые, перпендикулярные одной и той же прямой, параллельны.
Другие вопросы по теме Геометрия
Популярные вопросы
- 7. Знайдіть основу рівнобедреного трикутника, в якому бічна сторона і...
1 - Опыт 4. Определение анионов. Этот опыт необходимо про- водить в вытяжном...
3 - Знайти точки, які рівно віддалені від точок М, К і В, які не лежать на...
1 - №1733. Автомобіль протягом t годин їхав зі швидкістю 85 км/год. Склади...
1 - Підготувати проект на одну з заданих тем (писаний від руки з малюнками...
1 - Чому троянда приховувала свою любов до Маленького принца...
2 - КОМУ НЕ ТЯЖЕЛО НАКИДАТЬ ПАРУ РЕЧЕНЬ НА УКРАИНСКОМ ТОЛЬКО НЕ С ИНЕТА Поміркуй...
3 - Написати опис села в якесь свято в 3000- ному році...
2 - У багатьох соцмережах, крім уподобайок (лайків), є дизлайки (зна- чок...
1 - Укажіть рівняння для розв язування задачі якщо від числа 0,75 відняти...
3
Давайте разберем каждый шаг доказательства более подробно:
1. В этом шаге доказательства используется факт, что сумма углов треугольника равна 180°. В условии говорится, что угол <3 между прямыми AB и CD равен углу <6. Данное утверждение следует из условия задачи. Далее говорится, что угол
2. В этом шаге используется факт о вертикальных углах. Говорится, что угол СКА (обозначен как b) равен углу <3, так как они являются вертикальными углами (лежат на одной линии). Также угол
3. В этом шаге говорится о прямом треугольнике СКА. Если треугольник СКА прямоугольный (то есть имеет прямой угол), то треугольник DKB (со сторонами DK, DB и BK) также будет прямоугольным, потому что угол
4. В этом шаге используется первый признак параллельности прямых. Говорится, что если прямая AB перпендикулярна (образует прямой угол) к прямой b, то они параллельны. Доказательство этого факта не приводится в данном тексте.
Таким образом, доказательство показывает, что если треугольник СКА является прямоугольным и угол <3 равен углу <6, то прямая AB параллельна прямой b.
Это доказательство основывается на основных свойствах углов и треугольников, а также на основных фактах о параллельных и перпендикулярных прямых. Оно представлено шаг за шагом, чтобы сделать решение понятным для школьника и помочь ему разобраться в логике доказательства.