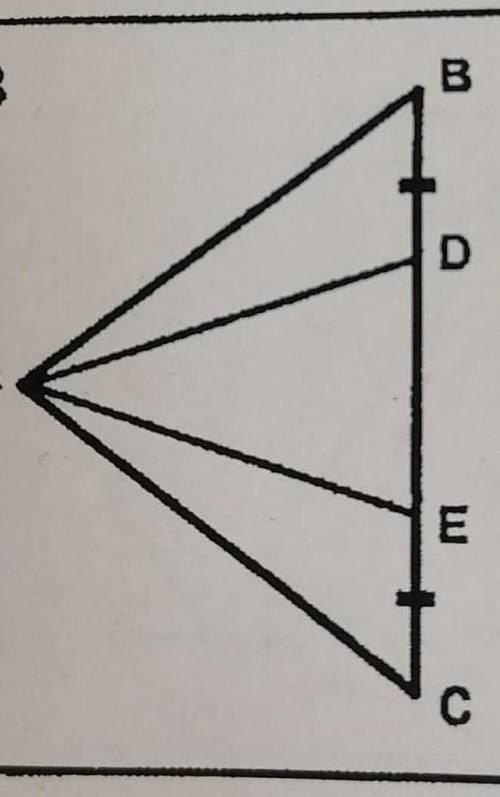
Доказать - треугольник АBC- равнобедренный​

Чтобы доказать, что треугольник АВС равнобедренный, нам нужно использовать условия равенства сторон и углов в треугольнике. Равнобедренный треугольник имеет две равные стороны и два равных угла.

1. По условию задачи, мы знаем, что сторона АВ равна стороне СВ.

2. Нам нужно доказать, что угол В равен углу С. Проверим это.

3. Рассмотрим треугольник АВС. Мы можем заметить, что у нас уже есть одно равенство сторон АВ = СВ (условие 1).

4. Если мы докажем, что угол А равен углу С (так как если два угла равны между собой, то третий угол в треугольнике также равен), то мы сможем заключить, что треугольник АВС равнобедренный.

5. Рассмотрим треугольник АВС и треугольник ВСА. Найдем их углы:

Угол ВАС - это угол между сторонами АВ и ВС.
Угол Д - это угол между сторонами АС и ВС.
Угол В - это угол между сторонами ВА и ВС.

6. Известно, что в треугольнике сумма всех углов равна 180 градусов. Поэтому угол Д + угол ВАС + угол В = 180 градусов.

7. Учитывая, что угол ВАС равен углу ВСА (это следует из условия равенства сторон АВ = СВ), мы можем переписать предыдущее равенство как угол Д + угол ВСА + угол В = 180 градусов.

8. Угол Д + угол ВСА + угол В = 180 градусов является уравнением для треугольника АВС.

9. По свойству треугольника, сумма углов в треугольнике равна 180 градусов.

10. Из пункта 9 мы можем заключить, что угол ВСА + угол Д + угол В = 180 градусов.

11. Так как угол ВСА равен углу ВАС (снова из условия равенства сторон АВ = СВ), мы можем переписать предыдущее равенство как угол ВАС + угол Д + угол В = 180 градусов.

12. Из пункта 11 мы можем заключить, что угол ВАС + угол В + угол Д = 180 градусов.

13. Сравнивая пункты 7 и 13, мы видим, что у нас есть уравнение угла и пусть равно 180 градусов.

14. Значит, уголи у треугольника АВС равны: угол А = угол С и угол В = угол А.

15. Значит, треугольник АВС является равнобедренным, так как у него две равные стороны АВ и СВ и два равных угла А и С, или угол В.

Таким образом, мы доказали, что треугольник АВС равнобедренный, так как у него есть две равные стороны и два равных угла.