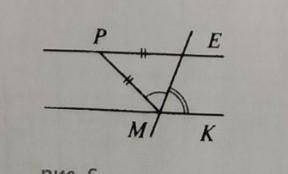
Доказать РЕ||МК
(Расписать типо как решать )

Для доказательства того, что РЕ||МК, нам понадобятся определения и свойства параллельных линий и транзитивности параллельности.

1. Определение: Две прямые линии называются параллельными, если они лежат в одной плоскости и не пересекаются, даже если продлить их до бесконечности.

2. Свойство: Если две прямые, А и Б, параллельны третьей прямой, С, то А и Б будут параллельны друг другу.

Теперь, давайте рассмотрим наши прямые:

1. По картинке, мы видим, что прямая РЕ и прямая МС пересекаются в точке А.
2. Давайте предположим, что РЕ и МС не параллельны друг другу.
3. Согласно свойству, упомянутому ранее, если РЕ и МС параллельны, то они также параллельны третьей прямой, например, прямой АС.
4. Но у нас есть противоречие, потому что изображение показывает, что РЕ и МС пересекаются в точке А, а не параллельны.
5. Из этого противоречия следует, что наше предположение было неверным.
6. Следовательно, РЕ и МС должны быть параллельными прямыми.

Таким образом, мы доказали, что РЕ и МС являются параллельными прямыми (РЕ||МК).