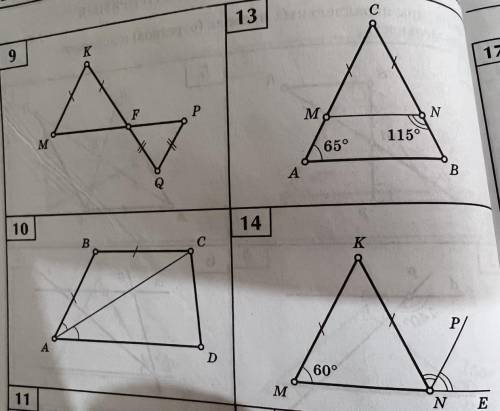
Доказать параллельность прямых

Для того чтобы доказать параллельность прямых, мы должны использовать определение параллельных прямых.

Определение: Две прямые называются параллельными, если они не имеют общих точек или имеют общую точку, но расстояние между ними постоянно.

Итак, у нас дана двумерная плоскость с двумя прямыми. Для начала, давайте обозначим точки на этих прямых. По условию, наша первая прямая обозначается буквой "а" и проходит через точки А и В, а вторая прямая обозначается буквой "б" и проходит через точки С и Д.

Теперь давайте проверим, пересекаются ли эти прямые. Если мы найдем общую точку между прямыми, то это будет означать, что они не параллельны.

Для этого нам нужно найти уравнения прямых "а" и "б". Уравнение прямой может быть записано в форме y = mx + b, где m - коэффициент наклона, b - свободный член. Чтобы найти уравнения прямых, нам понадобятся координаты точек А, В, С и Д.

Точка А имеет координаты (1, 2), точка В - (3, 7), точка С - (2, 4), а точка Д - (4, 9).

Теперь можно найти коэффициенты наклона и свободные члены для каждой прямой. Если коэффициенты наклона и свободные члены у прямых "а" и "б" равны, то это будет означать, что прямые параллельны.

Найдем уравнение прямой "а":
m = (7-2)/(3-1) = 5/2
Заметим, что точка (1, 2) принадлежит прямой "а", поэтому подставим ее в уравнение:
2 = (5/2)*1 + b
2 = 5/2 + b
b = 2 - 5/2
b = -1/2

Таким образом, уравнение прямой "а" имеет вид: y = (5/2)x - 1/2

Аналогично найдем уравнение прямой "б":
m = (9-4)/(4-2) = 5/2
Заметим, что точка (2, 4) принадлежит прямой "б", поэтому подставим ее в уравнение:
4 = (5/2)*2 + b
4 = 5 + b
b = 4 - 5
b = -1

Таким образом, уравнение прямой "б" имеет вид: y = (5/2)x - 1

Мы получили уравнения прямых "а" и "б". Теперь сравним их коэффициенты наклона и свободные члены. Они оба равны (5/2) и (-1/2) соответственно.

Следовательно, коэффициенты наклона и свободные члены у прямых "а" и "б" равны, что значит, что прямые параллельны.

Таким образом, мы доказали, что прямые "а" и "б" параллельны.