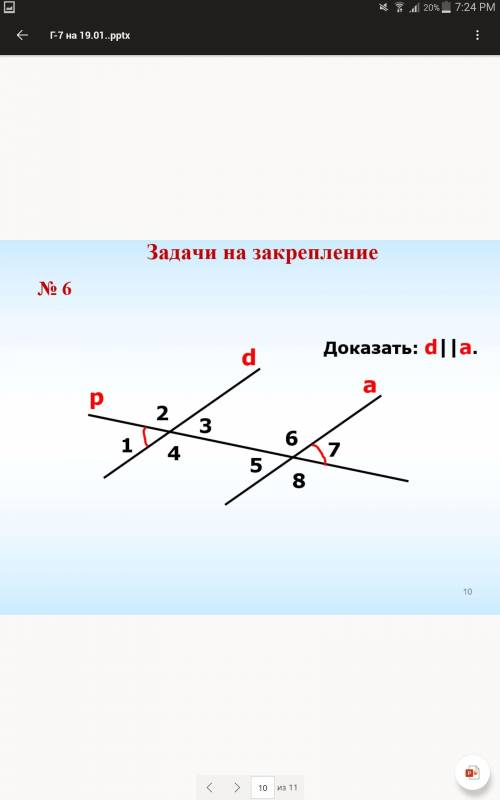
Доказать: d || a (d параллельно a) чертеж в фото. Заранее
Другие вопросы по теме Геометрия
Популярные вопросы
- Какой смысл вы видите в борьбе властей с «космополитами»?...
2 - Какой характер носили отношения СССР со странами народной демократии в...
3 - Приведите примеры гонений сталинского руководства на учёных, деятелей литературы,...
3 - Что нового появилось в отношениях КПСС и зарубежных компартий после окончания...
1 - Назовите достижения отечественной науки и культуры первых послевоенных...
2 - Какие изменения в международном положении СССР произошли после Второй мировой...
1 - Каково значение Сталинградской битвы в ходе Второй мировой войны?...
1 - Каково значение Тегеранской конференции?...
2 - Приведите конкретные примеры усиления административно-командной системы...
2 - Почему усилия властей были сосредоточены на разгроме новых научных направлений:...
2
Объяснение:
За умовою кут 1 і кут 7 — рівні , за теоремою , якщо різносторонні кути утворені перетином прямої ( січної)двох інших прямих , то ці прямі паралельні
Определение гласит, что две прямые прямые д = (d1, d2) и а = (a1, a2) на плоскости параллельны, если и только если их направляющие векторы пропорциональны друг другу.
Направляющий вектор для линии d обозначим как v(d) = (d1, d2). Мы можем использовать две точки на линии d для вычисления вектора направления:
v(d) = (x2 - x1, y2 - y1)
Возьмем для примера две точки, лежащие на линии d из данного чертежа на фото. Я выбираю точки A и B:
A(x1, y1) = (1, 2)
B(x2, y2) = (3, 4)
Тогда вектор направления d равен:
v(d) = (3 - 1, 4 - 2)
= (2, 2)
Теперь рассмотрим вектор направления линии а, v(а) = (а1, а2). Используя аналогичный подход, мы можем выбрать две точки на линии а и вычислить их вектор направления.
Выберем точки С и D:
C(x3, y3) = (2, 1)
D(x4, y4) = (4, 3)
Тогда вектор направления а будет:
v(а) = (4 - 2, 3 - 1)
= (2, 2)
Теперь нам нужно проверить, пропорциональны ли векторы направления d и а.
Для этого мы вычисляем их отношение, делая соответствующие деления компонент векторов:
(2/2) = (2/2)
У нас получается одна и та же дробь, что означает, что эти векторы направления пропорциональны.
Исходя из определения параллельных прямых, мы можем сделать вывод, что прямая d параллельна прямой а.
Таким образом, мы доказали, что d || a, основываясь на определении параллельных прямых и сравнении их векторов направления.