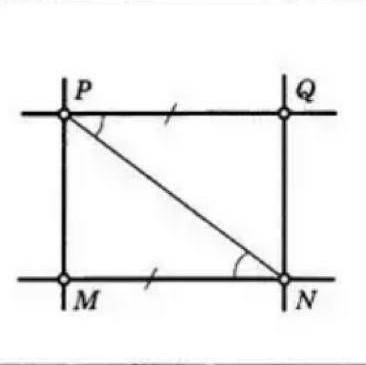
Доказать, что прямые параллельны по возможности дано напишите
Другие вопросы по теме Геометрия
Популярные вопросы
- При каком условии тело будет плавать? 1) Сила Архимеда равна силе тяжести...
2 - Запиши 5 любых предложений из упражнения 2 в отрицательной форме...
1 - РЕШИТЕ В ВИДЕ УРАВНЕНИЯ сумму чисел 165 и 633 уменьшили в несколько раз...
3 - Жер өз осінен айналуының нәтиежесінде Мен АуысадыКөп нүктенің орнына...
1 - Господа физики, 10 класс с задачей. Плоский конденсатор с площадью пластины...
1 - с номерами 2 и 5. Буду очень благодарна!...
1 - Какие последствия имели разделы Польшы для Украины ? Почему украинские...
2 - А. укажите фазы экономичемкого цикла.Б. выделите границы одного экономического...
3 - На рисунке представлен график зависимости скорости v от времени t для...
1 - В прямоугольном треугольнике АВС с гипотенузой ВС=16см,угол С=60°. Найдите...
1
Дано:
- Внутренние углы 1 и 2 являются соответственными углами, значит, они равны между собой: угол 1 = угол 2. (Аксиома соответственных углов)
- Угол 3 — внутренний угол суммы, состоящей из углов 1 и 2: угол 1 + угол 2 = угол 3. (Аксиома суммы углов)
- Угол 3 — смежный угол с углом 4, значит, они дополнительные: угол 3 + угол 4 = 180 градусов. (Аксиома дополнительных углов)
- По условию, угол 4 равен 107 градусам: угол 4 = 107 градусов.
Доказательство:
1. Если угол 1 = угол 2 и угол 4 = 107 градусов, то по аксиоме суммы углов угол 1 + угол 2 + угол 4 = угол 3 + угол 4.
2. Подставим вместо угла 1 угол 2: угол 2 + угол 2 + угол 4 = угол 3 + угол 4.
3. Упростим уравнение: 2 * угол 2 + угол 4 = угол 3 + угол 4.
4. Уберем угол 4 с обеих сторон: 2 * угол 2 = угол 3.
5. По свойству соответственных углов угол 2 равен углу 3: угол 2 = угол 3.
6. Подставим это равенство в предыдущее уравнение: 2 * угол 2 = угол 2.
7. Упростим уравнение: 2 = 1.
8. Получили противоречие, так как 2 не равно 1.
9. Следовательно, наше предположение о параллельности прямых было неверным.
Таким образом, прямые не являются параллельными.