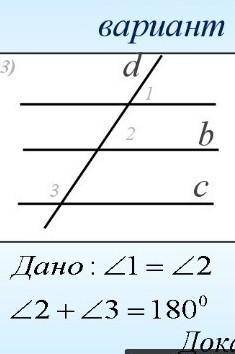
Доказать: что a паралельно b​

Чтобы доказать, что отрезок a параллелен отрезку b, мы можем использовать теорему о параллельных линиях и соответствующих углах.

Первым шагом нам нужно найти соответствующие углы между линиями a и b. В данной задаче есть два угла между этими линиями - угол X и угол Y.

Угол X и угол Y являются вертикальными углами, так как они лежат на пересекающейся прямой (боковая сторона треугольника ABC). Вертикальные углы равны между собой, поэтому угол X и угол Y равны.

Далее, мы обратимся к теореме о параллельных линиях и соответствующих углах, которая гласит: если углы, образованные пересекающимися прямыми и параллельными линиями, равны, то эти линии параллельны.

Так как угол X и угол Y равны (ведь они вертикальные углы), то мы можем сделать вывод, что линии a и b параллельны друг другу.

Таким образом, мы доказали, что отрезок a параллелен отрезку b, используя теорему о параллельных линиях и соответствующих углах и равенство вертикальных углов.