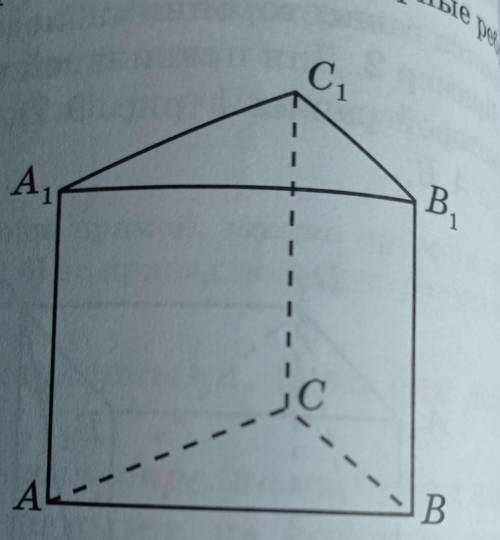
Для правильной треугольной призмы abca1b1c1 укажите ребра перпендикулярные ребру bb1​

AB,BC,AC, A1B1,B1C1,A1C1

Объяснение:

Чтобы найти ребра, перпендикулярные ребру bb1 в треугольной призме abca1b1c1, давайте рассмотрим структуру данной призмы.

В треугольной призме у нас есть основание abc и верхнее основание a1b1c1. Здесь оба основания — треугольники.

Изображение показывает, что основания расположены параллельно друг другу и вершины основания abc соединены с соответствующими вершинами верхнего основания a1b1c1. Обозначим верхние вершины a1, b1 и c1, соответственно.

Ребра перпендикулярные ребру bb1 будут проходить через вершины b и b1 и перпендикулярны этому ребру, что означает, что они встречаются в прямом углу с ребром bb1.

Школьнику может быть полезно представить себе треугольные призмы и представить, что некоторые линии проходят прямо через вершины.

Теперь, чтобы определить, какие именно ребра являются перпендикулярными к ребру bb1, нужно отыскать те ребра, которые проходят через вершины b и b1 и пересекаются с ребром bb1 под прямым углом. В геометрии такие ребра называются высотами или перпендикулярами.

В треугольной призме abca1b1c1 высотами, перпендикулярными ребру bb1, будут являться ребра, проходящие через вершины b и b1 и параллельные основаниям abc и a1b1c1.

Таким образом, ребра ad и a1d1 будут перпендикулярными ребру bb1 в данной треугольной призме abca1b1c1.

Вот пошаговое решение:

1. Изобразите треугольную призму abca1b1c1 соответствующим образом.
2. Найдите вершину b и b1 в призме.
3. Найдите ребро bb1, которое соединяет вершину b и b1.
4. Найдите ребра, которые проходят через вершины b и b1 и параллельные основаниям треугольных оснований abc и a1b1c1. Эти ребра будут перпендикулярными ребру bb1.
5. Обозначьте найденные ребра как ad и a1d1.

Надеюсь, это решение понятно школьнику! Если у него возникнут ещё вопросы, буду рад помочь!