Для измерения высоты дерева можно использовать описанный в книге Я.И. Перельмана "Занимательная геометрия " Он основан на равенстве угла падения и угла отражения света. Для этого на некотором расстоянии от измеряемого дерева,
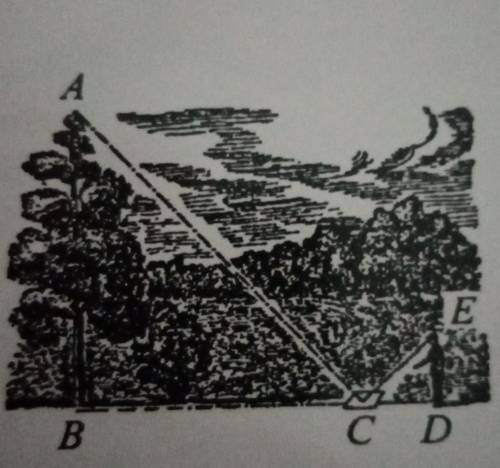
на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева.
Определите высоту дерева, изображенного на рисунке, если
рост человека составляет 1,8 м, а в результате измерений полу-
чено: ВС = 6 м, CD = 1,5 м.
​

Для решения данной задачи нам понадобятся знания о геометрии и правилах отражения света.

1. Рассмотрим треугольник BCD. В этом треугольнике мы знаем стороны BC и CD: BC = 6 м и CD = 1,5 м.

2. В треугольнике BCD можно использовать теорему Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Здесь гипотенуза - это отрезок BD, а катеты - это отрезки BC и CD.

3. Применяя теорему Пифагора, найдём длину отрезка BD:
BD^2 = BC^2 + CD^2
BD^2 = 6^2 + 1.5^2
BD^2 = 36 + 2.25
BD^2 = 38.25
BD = √38.25
BD ≈ 6.18 м

4. Теперь рассмотрим треугольник ABD. В этом треугольнике мы знаем сторону AB, которая равна росту человека и составляет 1.8 м, и сторону BD, которую мы посчитали на предыдущем шаге и получили около 6.18 м.

5. Мы можем использовать тригонометрию, а именно тангенс угла, чтобы найти высоту дерева. Тангенс угла можно определить как отношение противолежащего катета к прилежащему катету. В данном случае, противолежащим катетом является высота дерева, а прилежащим катетом - отрезок AB.

6. Мы можем записать уравнение, используя тангенс угла:
тангенс угла A = высота дерева / AB

7. Подставим известные значения:
тангенс угла A = высота дерева / 1.8
тангенс угла A = высота дерева / 1.8

8. Так как нам известен тангенс угла A, мы можем найти высоту дерева, используя обратную функцию тангенса. Обратная функция тангенса называется арктангенс и обозначается как atan. Тогда мы можем записать уравнение:
высота дерева = 1.8 * арктангенс (тангенс угла A)

9. Найдем тангенс угла A, используя отношение прилежащего и противолежащего катета в треугольнике ABD:
тангенс угла A = AB / BD
тангенс угла A = 1.8 / 6.18

10. Подставим значение тангенса угла A в формулу:
высота дерева = 1.8 * арктангенс (1.8 / 6.18)

11. Вычислим арктангенс (1.8 / 6.18) с помощью калькулятора или таблицы тригонометрических значений.
Округлим значение до двух десятичных знаков и получим приближенное значение высоты дерева.

Таким образом, мы можем использовать данные измерений (BC = 6 м, CD = 1,5 м) и рост человека (1,8 м) для определения высоты дерева. Окончательный ответ будет зависеть от численного значения арктангенса (1.8 / 6.18).