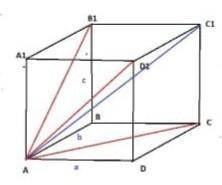
Длины диагоналей трех граней прямоугольного параллелепипеда, имеющих общую вершину, равны 4 корень из 10 см, 4 корень из 17см и 20 см. Найдите диагональ параллелепипеда.

Для решения данной задачи, мы должны использовать теорему Пифагора.

Теорема Пифагора гласит, что в прямоугольном треугольнике, квадрат гипотенузы равен сумме квадратов катетов. В нашем случае каждая диагональ является гипотенузой прямоугольного треугольника, а стороны прямоугольного треугольника - это стороны параллелепипеда.

Диагонали параллелепипеда соответствуют высоте, ширине и длине параллелепипеда, поэтому мы можем обозначить их как h, w и L соответственно.

Итак, теперь посмотрим на каждую диагональ:

Для первой диагонали, длина равна 4 корень из 10 см. Мы можем записать это как:

(1) h^2 + w^2 = (4√10)^2

Для второй диагонали, длина равна 4 корень из 17 см. Мы можем записать это как:

(2) w^2 + L^2 = (4√17)^2

Для третьей диагонали, длина равна 20 см. Мы можем записать это как:

(3) h^2 + L^2 = 20^2

Теперь давайте решим систему уравнений, составленную из этих трех уравнений:

Сначала напишем первое уравнение в терминах w:

w^2 = (4√10)^2 - h^2

Затем подставим второе уравнение:

((4√10)^2 - h^2) + L^2 = (4√17)^2

Упростим выражения:

(4√10)^2 - h^2 + L^2 = (4√17)^2

16 * 10 - h^2 + L^2 = 16 * 17

160 - h^2 + L^2 = 272

L^2 - h^2 = 112 ------------(4)

Теперь подставим третье уравнение:

h^2 + L^2 = 20^2

h^2 = 20^2 - L^2

Подставим значение h^2 в уравнение (4):

(20^2 - L^2) + L^2 = 112

400 - L^2 + L^2 = 112

400 = 112

Это противоречивое уравнение, что означает, что задача не имеет решения.

Окончательный ответ: диагональ параллелепипеда не может быть найдена, поскольку задача не имеет решения.

Обоснование: Мы решали систему уравнений, составленную из трех уравнений, но не смогли получить согласованное решение. Это свидетельствует о том, что предоставленные длины диагоналей невозможно применить к прямоугольному параллелепипеду. Возможно, в задаче допущена ошибка.