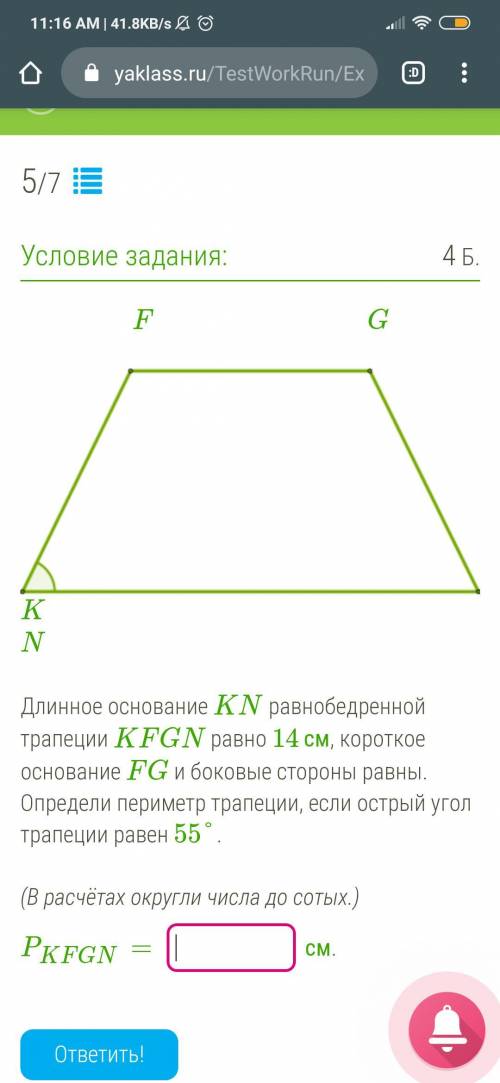
Длинное основание KN равнобедренной трапеции KFGN равно 14 см, короткое основание FG и боковые стороны равны. Определи периметр трапеции, если острый угол трапеции равен 55°.

(В расчётах округли числа до сотых.)
PKFGN=
см.

Для решения данной задачи, нам понадобятся знания о свойствах равнобедренных трапеций и треугольников.

Обозначим длину короткого основания FG как x (см). Также обратим внимание, что боковые стороны трапеции равны, поэтому сторона KG равна стороне FN.

Известно, что угол KFG = 55°. Так как в равнобедренной трапеции основания параллельны, то угол NKG (также острый угол) равен 55°.

Таким образом, получаем прямоугольный треугольник KFG, в котором гипотенуза KN равна 14 см, угол KFG равен 55° и катет FG равен x (см).

Для нахождения периметра трапеции, нам нужно найти длины всех сторон.

1. Найдем сторону KG (см):
В прямоугольном треугольнике KFG, используя тригонометрический соотношение косинуса, получаем:
cos(55°) = FG / KN
Подставим известные значения:
cos(55°) = x / 14
x = 14 * cos(55°)

2. Так как боковые стороны трапеции равны, то сторона KG (см) также равна стороне FN.

3. Найдем стороны FG и GN:
FG = x (см)
GN = FN = KG = 14 * cos(55°) (см)

4. Найдем периметр трапеции PKFGN:
Поскольку трапеция имеет две параллельные стороны FG и KN:
периметр трапеции = FG + GN + PK + KN
Периметр можно найти, используя найденные значения сторон:
периметр трапеции = x + 14 * cos(55°) + PK + 14

Все значения, кроме PK, мы уже нашли. Осталось найти PK.

5. Найдем сторону PK (см):
Из определения трапеции следует, что PK = GN - FG.
Подставим известные значения:
PK = (14 * cos(55°)) - x

Итак, мы можем найти периметр трапеции, подставив найденные значения:
периметр трапеции = x + 14 * cos(55°) + (14 * cos(55°)) - x + 14

Упростим это выражение:
периметр трапеции = 2 * 14 * cos(55°) + 28

Таким образом, периметр трапеции PKFGN равен 2 * 14 * cos(55°) + 28 см, где cos(55°) - это значение косинуса 55°.

Для получения точного значения периметра, необходимо вычислить значение косинуса 55° и выполнить все математические операции.