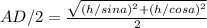Диалональ равнобедренной трапеции перпендикулярна к боковой стороне а угол между боковой стороной и большей основы трапеции равняеться а.найдите радиус круга вписаного вокруг трапеции если ее высота
равняеться h

нам дана трапеция ABCD в которой угол между диагональю и боковой стороной равен 90. (ABD=90)

мы будем решать задачу отталкиваясь от треугольника ABD, который также является вписанным в окружность

известно что если треугольник прямоугольный то радиус описанной окружности лежит на середине гипотенузы и равен  половине гипотенузы

значит нм и надо ее найти

она равна AD=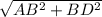 

AB=h/sina     BD=tga*AB=tga*h/sina=h/cosa 

отсюда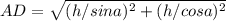  

ну и радиус соответственно R=