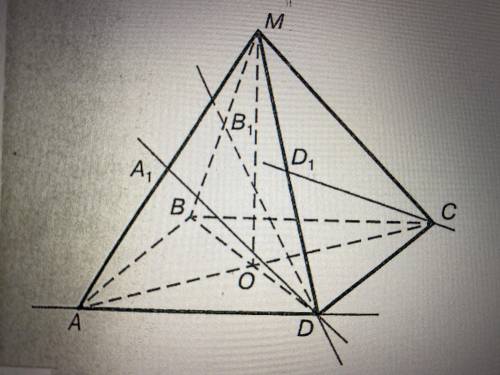
Диагональным сечением правильной пирамиды MABCD является равносторонний треугольник. Точка D1-середина ребра MD. Найдите углы, которые образуется прямая CD1 со следующими прямыми.
1) AD
2) DB1, точка B1 которой- середина ребра MB
3) DA1, точка А1 которой- середина ребра МА
Можно с полным объяснением.

Чтобы найти углы, которые образует прямая CD1 с прямыми AD, DB1 и DA1, нам понадобится использовать свойства геометрических фигур и знания о геометрических преобразованиях. Давайте рассмотрим каждый случай по отдельности.

1) Угол между прямыми CD1 и AD. Для этого нам понадобится знание о свойствах параллельных прямых. Так как AD является ребром пирамиды, то его можно считать параллельным треугольнику ABCD, так как они лежат в одной плоскости. Из условия задачи известно, что сечение MABCD является равносторонним треугольником. Значит, у нас есть равные углы в треугольнике, и все его стороны равны. Так как MD1 является средней линией равностороннего треугольника ABC, то она параллельна одной из его сторон. Таким образом, мы можем сказать, что CD1 параллельна AD. Из свойств параллельных прямых можно сделать вывод, что углы, образуемые этими прямыми, равны. Значит, в данном случае угол между прямыми CD1 и AD равен углу между прямыми MD1 и AD. Так как MD1 является средней линией равностороннего треугольника ABC, то угол между MD1 и AD равен 60 градусов (так как каждый угол равностороннего треугольника ABC равен 60 градусов). Значит, угол между CD1 и AD также равен 60 градусов.

2) Угол между прямыми CD1 и DB1. Также для решения этого случая нам понадобится знание о свойствах параллельных прямых. Рассмотрим треугольник DB1M. Так как B1 является серединой ребра MB, то DB1 параллельна DM (так как B1D будет являться средней линией равнобедренной трапеции DMAB1). Также из условия задачи известно, что MD1 является средней линией равностороннего треугольника ABC. Значит, MD1 и DM также параллельны. Из свойств параллельных прямых можно сделать вывод, что углы, образуемые этими прямыми, равны. Значит, в данном случае угол между прямыми CD1 и DB1 равен углу между прямыми MD1 и DB1. Так как MD1 является средней линией равностороннего треугольника ABC, то угол между MD1 и DB1 также равен 60 градусов (так как каждый угол равностороннего треугольника ABC равен 60 градусов). Значит, угол между CD1 и DB1 также равен 60 градусов.

3) Угол между прямыми CD1 и DA1. В данном случае нам необходимо использовать свойство перпендикулярных прямых. Рассмотрим сечение MABCD и треугольник DA1M. Так как A1 является серединой ребра MA, то DA1 параллельна MB (так как A1B будет являться средней линией равнобедренной трапеции MAB1A1). Также из условия задачи известно, что MD1 является средней линией равностороннего треугольника ABC. Значит, MD1 и DM также параллельны. Так как DM и MB параллельны, а DA1 и DA - это одна и та же прямая, то DA1 и MB перпендикулярны. Из свойств перпендикулярных прямых можно сделать вывод, что углы, образуемые этими прямыми, равны 90 градусов. Значит, в данном случае угол между прямыми CD1 и DA1 равен 90 градусов.

Таким образом, углы, которые образуют прямая CD1 со следующими прямыми, равны:
1) Угол между CD1 и AD - 60 градусов.
2) Угол между CD1 и DB1 - 60 градусов.
3) Угол между CD1 и DA1 - 90 градусов.