1. Геометрия
  2. Диагонали ромба 6 см и 14 см.

Диагонали ромба 6 см и 14 см. Найдите сторону и S ромба. Можно с условием, рисунком, ну и решением!

mariapogorelova mariapogorelova    3   15.12.2021 22:12    0

Ответы
mannanova0202 mannanova0202  07.02.2022 02:36

Дано : Четырёхугольник ABCD - ромб.

АС = 6 см, BD = 14 см.

Найти :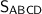 \sf S_{ABCD} = ?

Сторона = ?

▌Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.

AC⊥BD, AC∩BD = O ⇒ СО = АО = AC : 2 = 6 см : 2 = 3 см, BO = DO = BD : 2 = 14 см : 2 = 7 см.

Неважно какую сторону ромба мы будем искать, так как стороны ромба между собой равны (по определению).

Рассмотрим прямоугольный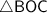 \sf \triangle BOC (он прямоугольный потому что ∠ВОС = 90°).

По теореме Пифагора -

\sf BO^{2} +CO^{2} =CB^{2}

7² + 3² = СВ²

СВ² = 49 + 9  = 58 ⇒ СВ =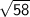 \sf \sqrt{58} (см) - сторона ромба.

▌Площадь ромба равна половине произведения его диагоналей.

\sf S_{ABCD} = \frac{AC*BD}{2} = \frac{6*14}{2} = 3*14 = 42 (см²).

ответ : 42 см²,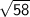 \sf \sqrt{58} см.


Диагонали ромба 6 см и 14 см. Найдите сторону и S ромба. Можно с условием, рисунком, ну и решением!
ПОКАЗАТЬ ОТВЕТЫ
vika02bel vika02bel  07.02.2022 02:36

АВ=

\sqrt{58}

см

Площадь ромба: 42 кв см

Объяснение:

Дано: АВСD ромб. BD = 6см, АС=14см

Найти: АВ, S(АВСD)

Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам.

Рассмотрим прямоугольный треугольник АВО(<О=90°)

Так как АО=ОС, ВО=ОD, то

АО=14:2=7см, ВО=6:2=3см.

П теореме Пифагора найдём гипотенузу АВ:

ab = \sqrt{ {ao}^{2} + {bo}^{2} } = \sqrt{ {7}^{2} + { {3}^{2} } } = \\ \sqrt{49 + 9} = \sqrt{58}

Так как все стороны ромба равны, то сторона ромба равна:

\sqrt{58}

Площадь ромба находим через диагонали по формуле:

s = \frac{1}{2} \times d1 \times d2 = \frac{1}{2} \times 6 \times 14 = 42 \: {cm}^{2}


Диагонали ромба 6 см и 14 см. Найдите сторону и S ромба. Можно с условием, рисунком, ну и решением!
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
betmenduma betmenduma  17.09.2019 10:00
Выберите верные высказывания : а) если один из односторонних углов ,образованных при пересечении параллельных прямых секущей, равен 30 градусам , то и другой односторонний...
polinasparrow polinasparrow  22.04.2020 10:20
В прямоугольном треугольнике ABC с прямым углом A гипотенуза равна 5, а AC 4, найти косинус угла C и площадь треугольника....
innarudenkoco innarudenkoco  22.04.2020 10:20
РЕШИТЬ Найдите координаты и абсолютную величину вектора с, если А) с = а+b Найдите вектор d Б) d = -3a Будут ли векторы а и d со направленными ответ обьясните...
03721 03721  22.04.2020 10:20
AB это диаметр окружности с центром O.Найдете угол CAO если.OA=OC=BC....
Victoriya1234567890 Victoriya1234567890  22.04.2020 10:20
Найти все неизвестные углы треугольника...
Лейла1994 Лейла1994  22.04.2020 10:20
В окружности проведены две хорды AB и CD, пересекающиеся в точке М. Известно что AB 15см, СМ 9см, МD 4 см, расстояние между точками А и С равно 11 см. Найдите острый угол,между...
Няшка9000 Няшка9000  22.04.2020 10:20
На листе бумаги сначала изобразили 3 пересекающиеся прямые (исходные прямые не пересекаются в одной точке), а затем 4 параллельные прямые. Как могут быть расположены эти...
Nastenka0003 Nastenka0003  22.04.2020 10:20
Дана треугольная пирамида вписанная в конус. в основании пирамиды лежит треугольник со сторонами 6,8 и 10см.образующая конуса равна 13.найти высоту конуса и площадь боковой...
Over003 Over003  08.05.2020 03:10
Задача 1.Правильная четырехугольная призма.Сторона основания =3. Объем призмы равен 45. Найти: 1)квадрат площади диагонального сечения 2)Площадь боковой поверхности 3)Площадь...
Яумницакрасотка Яумницакрасотка  08.05.2020 03:10
Правильная четырехугольная пирамида. Высота пирамиды=8.Высота боковой грани =10 Найти: Сторона основания Квадрат бокового ребра Объем Площадь полной поверхности...

Популярные вопросы