1. Геометрия
  2. Диагональ равносторонней трапеции

Диагональ равносторонней трапеции перпендикулярна боковой стороне, а угол между боковой стороной и большим основанием трапеции равен . Найдите радиус окружности, описанной вокруг
трапеции, если ее высота равна h.

Marinet1806 Marinet1806    1   04.08.2022 08:37    1

Ответы
Ольга5555555555 Ольга5555555555  04.08.2022 08:38

\displaystyle\frac{h}{{2\sin \alpha \cos \alpha }}=\displaystyle\frac{h}{{\sin 2\alpha }}

Объяснение:

Используя метрические соотношения в прямоугольном треугольнике из треугольника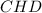 CHD получаем:

\sin \alpha = \displaystyle\frac{{CH}}{{CD}};

CD = \displaystyle\frac{h}{{\sin \alpha }}.

Тогда из треугольника ACD

\cos \alpha = \displaystyle\frac{{CD}}{{AD}};

AD = \displaystyle\frac{{CD}}{{\cos \alpha }} = \displaystyle\frac{h}{{\sin \alpha }}:\cos \alpha = \displaystyle\frac{h}{{\sin \alpha }} \cdot \displaystyle\frac{1}{{\cos \alpha }} = \displaystyle\frac{h}{{\sin \alpha \cos \alpha }}.

Описанная окружность трапеции одновременно является описанной окружностью вокруг прямоугольного треугольника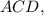 ACD, значит ее радиус равен половине гипотенузы:

R = \displaystyle\frac{{AD}}{2} = \displaystyle\frac{h}{{2\sin \alpha \cos \alpha }}.

Пользуясь знаниями по тригонометрии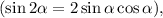 (\sin 2\alpha = 2\sin \alpha \cos \alpha ), можно записать ответ компактнее:

R = \displaystyle\frac{h}{{\sin 2\alpha }}.


Диагональ равносторонней трапеции перпендикулярна боковой стороне, а угол между боковой стороной и б
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
malenkayakreyz malenkayakreyz  02.03.2020 14:23
Решите найти угол А угол В угол С мне надо решение я знаю что есть ответ...
Dashakrasaveta Dashakrasaveta  02.03.2020 14:22
Дано трикутник а=30 б=21 Знайти С Кут А Кут Б...
nikitka1011 nikitka1011  02.03.2020 14:22
Металлический цилиндр, осевым сечением которого является квадрат, а радиус основания равен 2 дм, переплавлен в шар.Найдите радиус (дм) этого шара. Потерями металла...
gribvlad123 gribvlad123  02.03.2020 14:22
У трикутнику АВС відомо, що ∠ А = α, бісектриси зовнішніх кутів при вершинах В і С перетинаються в точці О. Знайдіть кут ВОС....
Student223 Student223  24.12.2019 14:26
Тест по . 8 класс. простой тест. много...
Noop1 Noop1  24.12.2019 14:27
Зточки а до площини альфа проведено перпендикуляр ав і похилі ас і ак. ас = 6 смкут між похилою і перпендикуляром дорівнює 30°. пряма ск перпендикулярна до проекції...
кристина2043 кристина2043  24.12.2019 14:30
Решить, плачу все , которые у меня есть. подробно с решением...
ssss13 ssss13  24.12.2019 14:31
Вычислите площадь трапеции abcd с основаниями ad u bc, если ad=20, bc=14, угол а-45 градусов, d 90 градусов...
tihon123123 tihon123123  24.12.2019 14:31
Abcda1b1c1d1-куб,dm=md1.найти угол между прямыми ad1 и bm.​...
Kennyssess Kennyssess  24.12.2019 14:31
50 . нужно подробное решение с дано​...

Популярные вопросы