Диагональ MP параллелограмма MNPQ равна 24 см. Из вершины Q в точку E, которая является серединой NP, проведен отрезок. Найдите отрезки, на которые диагональ MP делится отрезком QE.
Другие вопросы по теме Геометрия
Популярные вопросы
- Определите коэффициент увлажнения, если известно, что среднегодовое...
1 - Используя карты атласа Распределите реки России по бассейнам океанов...
2 - Сообщение про Красную книгу Татарсиана...
3 - Task1. Ex 1 p83 Look at the picture (p82) Answer the questions....
3 - НУЖНО НАПИСАТЬ ЭССЕ ПО АНГЛИЙСКОМУ (ПО ПЛАНУ) ...
2 - Почвы города Алматы и их особенности...
2 - До ть написати есе на тему чистіша від сльози вона хай буде будь-ласка...
2 - 4. О живом человеке или о памятнике говорит поэт? Стихотворение...
2 - В 1741 году началась война между Россией и Швецией, после того...
3 - Число равно самому себе умноженоиу на 7 - 18.Что это за число?...
3
8 и 16 см
Объяснение:
Обозначим О точку пересечения диагоналей параллелограмма, а точкой С пересечение отрезка QE с диагональю MP. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому ВО — медиана треугольника NPQ.
Отрезок QE также является медианой треугольника NPQ, точкой пересечения медианы делятся в отношении 2 : 1, считая от вершины. Поэтому
PC=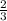 MP=
MP=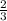 * 24= 8 см
* 24= 8 см
MC= 24-8=16 см