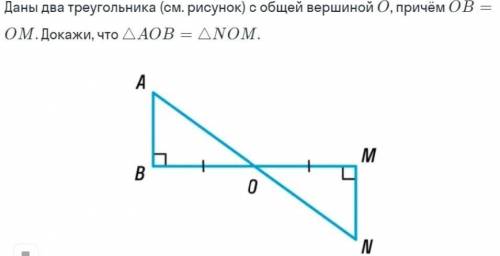
Даны 2 треугольника (см. рисунок) с общей вершиной - О, причем OB = OM. Докажите, что ∆AOB = ∆NOM.

Для начала, давайте разберемся с обозначениями. О, B и M - это вершины треугольников, изображенных на рисунке. Согласно условию, OB = OM, что означает, что отрезки OB и OM имеют одинаковую длину.

Нам нужно доказать, что треугольник AOB равен треугольнику NOM. Для этого мы можем использовать свойство треугольников, называемое "Критерий равенства треугольников по двум сторонам и углу между ними". Он гласит, что если два треугольника имеют две стороны, равные по длине, и угол между ними равен, то они равны.

Докажем, что стороны AO и NO равны по длине:

1. Обратимся к треугольнику AOM. У нас уже есть отрезки OB и OM с одинаковой длиной.
2. Рассмотрим треугольники AOB и NOM. Мы можем заметить, что стороны AO и NO являются продолжениями отрезков OB и OM соответственно.
3. Согласно условию, OB = OM, а следовательно, стороны AO и NO равны по длине.

Теперь рассмотрим угол AOB и угол NOM:

1. Мы знаем, что OB = OM, и значит треугольники AOM и BOM являются равнобедренными треугольниками, так как у них равны две стороны.
2. Рассмотрим угол AOM и угол BOM. Вышеуказанное свойство треугольников говорит нам, что если у двух треугольников две стороны равны и угол между ними равен, то эти треугольники равны.
3. Исходя из этого, угол AOM = угол BOM.

Таким образом, мы доказали, что треугольник AOB равен треугольнику NOM.