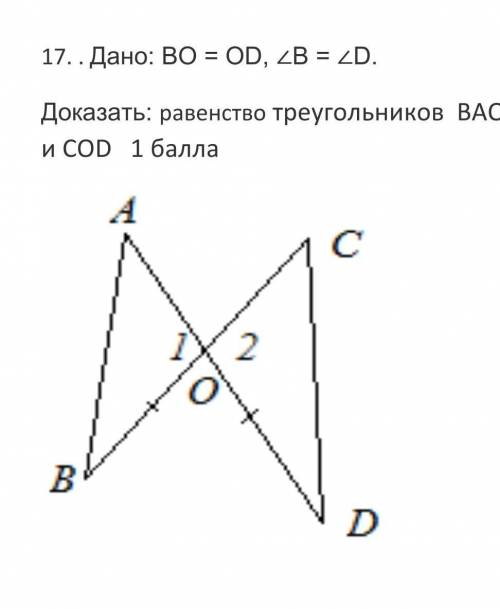
Дано: ВО = ОD, ∠В = ∠D.

Доказать: равенство треугольников ВАО и СОD

​

Чтобы доказать равенство треугольников ВАО и СОD, мы можем воспользоваться свойствами равенства треугольников - две стороны и угол между ними равны в двух треугольниках. Рассмотрим каждый элемент:

1. Дано, что ВО = ОD. Это значит, что сторона BO равна стороне DO.

2. Дано, что ∠В = ∠D. Это значит, что угол B равен углу D.

Теперь нужно показать, что стороны VA и SO равны, а также угол A и угол O равны.

3. Рассмотрим треугольник ВAO.

ВО и ОА - это две стороны треугольника ВАО.

У нас уже есть, что в треугольнике ВАО сторона BO равна DO. Также, из дано, мы знаем, что ВО = ОD.

Таким образом, у нас есть три стороны, которые равны: ВО = ОD, ВО = ОА и ОD = ОА. По свойству равенства треугольников, треугольник ВАО равен треугольнику ОDA.

4. Теперь рассмотрим треугольник СОD.

ОD и DA - это две стороны треугольника СОD.

Мы только что доказали, что треугольник ВАО равен треугольнику ОDA. Значит, стороны ОD и ОА равны, т.е. ОD = ОА.

Таким образом, у нас есть две равные стороны и один равный угол между ними: ОD = ОА, ОD = ОА и угол D = углу A. По свойству равенства треугольников, треугольник СОD равен треугольнику ОDA.

Итак, мы доказали, что треугольник ВАО равен треугольнику ОDA, и треугольник СОD равен треугольнику ОDA. Следовательно, треугольники ВАО и СОD также равны друг другу.