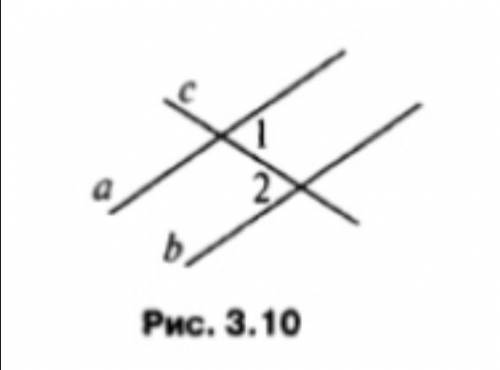
Дано: угол 1=32градуса, угол 2=32градуса
Доказать: a||b

Добрый день! С удовольствием помогу вам решить эту задачу.

Для доказательства, что прямые a и b параллельны, мы должны использовать информацию о заданных углах 1 и 2.

Первым шагом давайте построим вспомогательные линии и отметим все известные углы на данной фигуре:

1. Проведем линии, соединяющие вершины beiden треугольников с точкой пересечения прямых a и b. Назовем эту точку O.

2. Обозначим вершины двух треугольников следующим образом:
- Верхняя вершина левого треугольника: A
- Верхняя вершина правого треугольника: B
- Нижняя вершина левого треугольника: C
- Нижняя вершина правого треугольника: D

3. Потянем линию от вершины O и проведем ее параллельно стороне BC. Обозначим точку пересечения этой линии со стороной AB как E.

Сейчас у нас есть три треугольника: треугольник AOC, треугольник BOD и треугольник AEB.

Далее, нам понадобится обратить внимание на некоторые свойства треугольников.

Свойство 1: Внутренние углы треугольника AOC всегда суммируются до 180 градусов.
Свойство 2: Внутренние углы треугольника BOD всегда суммируются до 180 градусов.
Свойство 3: Внутренние углы треугольника AEB всегда суммируются до 180 градусов.

Теперь перейдем к доказательству:

Доказательство:
1. Угол 1 равен 32 градусам. Это значит, что угол AOC равен 180 - 32 = 148 градусов, так как углы треугольника всегда суммируются до 180 градусов.
2. Угол 2 равен 32 градусам. Это значит, что угол BOD равен 180 - 32 = 148 градусов.
3. Учитывая, что углы AOC и BOD равны, мы можем сделать вывод о том, что треугольники AOC и BOD равны по двум углам и стороне CO, так как линия a параллельна линии b.
4. Поскольку треугольники AOC и BOD равны, это означает, что сторона OA равна стороне OB, сторона OC равна стороне OD и углы ACO и BDO равны.
5. Проведем линию ED. По свойству параллельных линий мы знаем, что угол AEB равен углу ACO (по свойству соответственных углов).
6. Угол ACO равен 180 - 148 = 32 градусам.
7. Исходя из этого, угол AEB также равен 32 градусам.
8. Учитывая, что угол AEB равен углу 2 и уголу 1, мы можем сделать вывод о том, что линия ED параллельна линии a.

Таким образом, мы доказали, что линия ED || a и b.

они параллельны так как они накрест лежащие .

180° -32°=148°