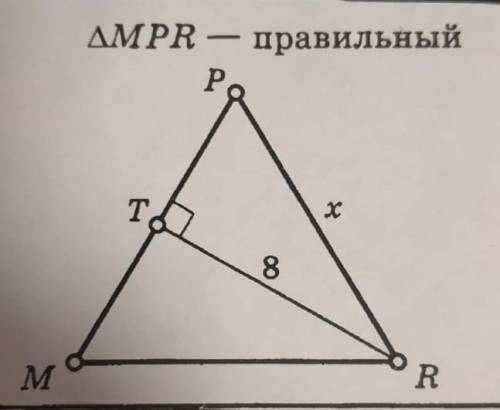
Дано треугольник mpr правильный TR равно 8 см Найдите PR​. (по теореме Пифагора)

1)180-90=90

P=60

R=30

2)30*2=60(R)

180-60=120

120:2=60(M)

3)TR//PR=8 см

Объяснение:

MR+RP+MP= P

8+8+8=24(P)

посмотри теорему в инете и представь свои числа, вроде 9 будет

Для решения данной задачи мы будем использовать теорему Пифагора, которая гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В данном случае мы имеем треугольник mpr, в котором TR является гипотенузой, а MP и PR - катетами. Мы знаем, что TR равно 8 см.

Сначала воспользуемся теоремой Пифагора для нахождения длины одной из сторон треугольника.

По теореме Пифагора:
TR^2 = MP^2 + PR^2

Заменяя известные значения наших сторон, получаем:
8^2 = MP^2 + PR^2

Решим это уравнение, чтобы найти PR.

64 = MP^2 + PR^2

Теперь нам нужно найти длину MP.

Мы знаем, что треугольник mpr является равносторонним треугольником, так как он правильный.
Это значит, что все его стороны равны.

Обозначим длину стороны mpr как x.

Таким образом, MP = PR = x.

Теперь вернемся к уравнению:

64 = MP^2 + PR^2

Подставим x вместо MP и PR:

64 = x^2 + x^2

64 = 2x^2

Разделим обе части уравнения на 2:

32 = x^2

Возьмем квадратный корень от обеих сторон:

√32 = √(x^2)

4√2 = x

Таким образом, длина одной из сторон треугольника mpr равна 4√2 см.

Теперь мы можем найти PR:

PR = x = 4√2 см.

Итак, PR равно 4√2 см.